NCERT Exemplar Solutions
Class 6 - Mathematics - Unit 9: Symmetry and Practical Geometry - Problems and SolutionsQuestion 63
Class 6 - Mathematics - Unit 9: Symmetry and Practical Geometry - Problems and Solutions
Question. 63
In Fig. 9.13, PQRS is a rectangle. State the lines of symmetry of the rectangle.
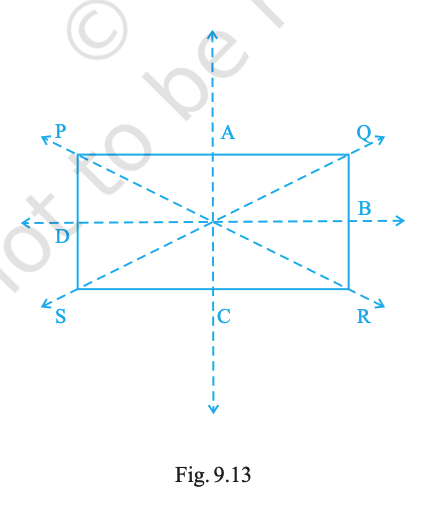
Answer:
AC and BD.
Detailed Answer with Explanation:
Explanation (Very Simple Steps)
Goal: We have a rectangle PQRS. We must tell which lines are its lines of symmetry.
-
What is a line of symmetry?
If you fold a shape along this line, both halves match exactly.( ext{Line of symmetry} Rightarrow ext{two identical halves on folding})
-
Look at the picture. Points A, B, C, D are the midpoints of the sides of the rectangle (as shown in the figure).
(A, C ext{ are midpoints on opposite sides})
(B, D ext{ are midpoints on the other pair of opposite sides})
-
First line of symmetry: Join the midpoints on the left and right sides.
( ext{Draw the line } AC)
( ext{This is a vertical line through the center})
Folding the rectangle along AC makes the left half sit exactly on the right half.
-
Second line of symmetry: Join the midpoints on the top and bottom sides.
( ext{Draw the line } BD)
( ext{This is a horizontal line through the center})
Folding the rectangle along BD makes the top half sit exactly on the bottom half.
-
Important check (diagonals): Are the diagonals lines of symmetry?
( ext{In a general rectangle: diagonals are NOT lines of symmetry})
( ext{Diagonals become symmetry lines only if it is a square})
Conclusion / Final Answer:
( ext{Lines of symmetry of rectangle } PQRS:~ AC ext{ and } BD.)