NCERT Exemplar Solutions
Class 6 - Mathematics - Unit 9: Symmetry and Practical Geometry - Problems and SolutionsQuestion 69
Class 6 - Mathematics - Unit 9: Symmetry and Practical Geometry - Problems and Solutions
Question. 69
Draw the images of points A and B in line l of Fig. 9.14 and name them as A′ and B′ respectively. Measure AB and A′B′. Are they equal?
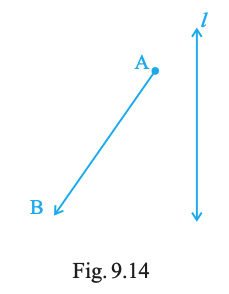
Answer:
Yes, AB = A′B′.
Detailed Answer with Explanation:
Solution (Very Beginner-Friendly)
We will first draw the mirror images of the points A and B in the line l. Then we will measure the lengths and compare.
-
Draw A′ (image of A in line l)
- With a set square or protractor, draw a short line from A to l that is perpendicular to l. Let it meet l at point P.
- Measure the distance AP with a ruler.
- On the other side of line l, along the same perpendicular, mark a point A′ so that the distance from P to A′ is the same as AP.
( AP perp l )
( PA' = PA )
-
Draw B′ (image of B in line l)
- Draw a perpendicular from B to l. Let it meet l at Q.
- Measure the distance BQ.
- On the other side of l, along the same perpendicular, mark B′ so that the distance from Q to B′ equals BQ.
( BQ perp l )
( QB' = BQ )
-
Measure the two segment lengths
- Use a ruler to measure the length AB.
- Use the ruler again to measure the length A′B′.
-
Compare
( AB stackrel{?}{=} A'B' )
You will find that the two lengths are equal.
( AB = A'B' )
Why are they equal?
- Reflecting (taking a mirror image) in a line is a distance-preserving move. This is also called an isometry.
- Each point and its image are the same distance from the mirror line and lie on a line perpendicular to it.
- Because the whole figure is “flipped” without stretching, the distance between A and B is the same as the distance between A′ and B′.
( ext{dist}(A,l) = ext{dist}(A',l) )
( ext{dist}(B,l) = ext{dist}(B',l) )
( herefore; AB = A'B' )
Note: If your measured values differ slightly, it is usually due to drawing or measuring errors. Re-check the perpendiculars and equal distances from the line l.
Answer: Yes, ( AB = A'B' ).