83. Bisect ∠XYZ of Fig. 9.22
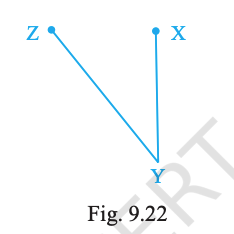
(angle XYZ)
What you need
- A compass
- A ruler (unmarked edge for straight line)
- A sharp pencil
- (Optional) A protractor to check the answer
Construction (step by step)
-
Put the compass pin at point Y.
Open the compass to a small, comfortable width (any convenient radius).
Draw one arc that cuts both arms YX and YZ.
Mark the cut points as A on YX and B on YZ.
(A in YX,quad B in YZ)
- Without changing the compass width, place the pin on A and draw a small arc in the interior of the angle.
- Again, without changing the width, place the pin on B and draw another small arc so that it meets the previous arc. Mark their intersection as P.
-
Use the ruler to draw a straight line from Y to P.
The line YP is the bisector of the angle.
(YP ext{ bisects } angle XYZ)
Reason (why this works)
We drew equal arcs with the same compass width. So the distances are equal.
(YA = YB)
(AP = BP)
Now look at triangles △YAP and △YBP:
(YA = YB)
(same arc from Y)(AP = BP)
(arcs drawn with equal radius)(YP)
is common
So the two triangles are congruent by SSS.
( riangle YAP cong riangle YBP)
Therefore the angles at Y on both sides of YP are equal.
(angle AYP = angle PYB)
This means YP divides the original angle into two equal parts.
(angle XYZ = angle AYP + angle PYB)
(angle AYP = angle PYB)
Check your construction
- Use a protractor to measure
(angle AYP)
and(angle PYB)
. They should be equal. - Or, keep the compass width the same and compare the arcs; both sides should match.
Result
Line YP is the bisector of (angle XYZ)