NCERT Exemplar Solutions
Class 6 - Mathematics - Unit 9: Symmetry and Practical Geometry - Problems and Solutions
Question 87

Question. 87

Draw an angle ABC of measure 45°, using ruler and compasses. Now draw an angle DBA of measure 30°, using ruler and compasses as shown in Fig. 9.23. What is the measure of ∠DBC?

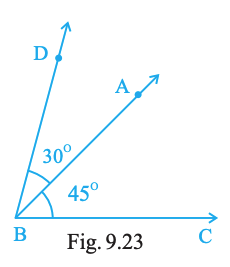
Answer:

∠DBC = 75°.

Detailed Answer with Explanation:

Step-by-step Explanation (Very Simple)

We are given:

(angle ABC = 45^circ)

(angle DBA = 30^circ)

We need to find the size of (angle DBC) (the angle from the ray (BD) to the ray (BC), both with vertex at (B)).

Think of the three rays from point B

  1. Ray (BA)
  2. Ray (BC) such that (angle ABC = 45^circ)
  3. Ray (BD) such that (angle DBA = 30^circ)

Move around point (B) in the same direction:

  • From (BD) to (BA): this turn is (30^circ).
  • From (BA) to (BC): this turn is (45^circ).

Add the two small turns

(angle DBA = 30^circ)

(angle ABC = 45^circ)

(angle DBC = angle DBA + angle ABC)

(angle DBC = 30^circ + 45^circ)

(angle DBC = 75^circ)

Answer: (angle DBC = 75^circ).

(Optional) How to construct the figure with ruler & compass

  1. Draw (angle ABC = 45^circ):
    • Draw a base line (BA).
    • At point (B), construct a right angle ((90^circ)) using perpendicular lines.
    • Bisect the (90^circ) angle to get (45^circ) and mark the ray (BC).
  2. Draw (angle DBA = 30^circ):
    • First construct (60^circ) at (B) (by forming an equilateral triangle with compass).
    • Bisect the (60^circ) angle to get (30^circ) and mark the ray (BD) on that side of (BA) shown in the figure.
  3. Read (angle DBC): This is the total turn from (BD) to (BC), which we calculated as (75^circ).
Open NCERT PDF
NCERT Exemplar Solutions Class 6 – Mathematics – Unit 9: Symmetry and Practical Geometry – Problems and Solutions | Detailed Answers