NCERT Exemplar Solutions
Class 6 - Mathematics - Unit 6: Mensuration - Problems and SolutionsQuestion 21
Class 6 - Mathematics - Unit 6: Mensuration - Problems and Solutions
Question. 21
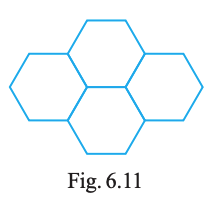
Four regular hexagons are drawn so as to form the design as shown in Fig. 6.11. If the perimeter of the design is 28 cm, find the length of each side of the hexagon.
Answer:
Length of each side of the hexagon = 2 cm
Detailed Answer with Explanation:
Perimeter means the total distance around the outside of a shape.
In the given figure, four regular hexagons are joined. Some sides touch each other inside, so they are not on the outside. We only count the outer (exposed) sides for the perimeter.
Carefully go around the outer boundary of the design and count the sides you see on the outside. From the figure, the number of outer sides is:
( ext{Number of exposed sides} = 14)
Let the length of each side of a hexagon be (;s) cm.
The perimeter (P) of the whole design equals the number of exposed sides multiplied by the side length:
[ P = 14 imes s ]
We are told the perimeter is (28) cm. So,
[ 14s = 28 ]
Divide both sides by (14):
[ s = rac{28}{14} ]
[ s = 2 ext{ cm} ]
Therefore, the length of each side of the hexagon is (2) cm.