NCERT Exemplar Solutions
Class 6 - Mathematics - Unit 9: Symmetry and Practical Geometry - Problems and Solutions
Question 72

Question. 72

Draw the images of the points A, B and C in the line m (Fig. 9.17). Name them as A′, B′ and C′, respectively and join them in pairs. Measure AB, BC, CA, A′B′, B′C′ and C′A′. Is AB = A′B′, BC = B′C′ and CA = C′A′?

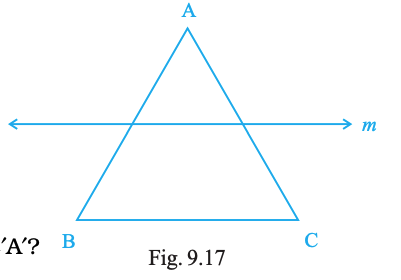
Answer:

Yes, Yes, Yes.

Detailed Answer with Explanation:

Explanation (Very Simple Steps)

We have three points A, B, C and a line m. We will draw their images in line m and name them A′, B′, C′. Then we will compare the lengths.

What you need

  • Ruler (scale)
  • Compass
  • Pencil
  • Protractor (optional)

Step 1: Reflect point A in line m

  1. Keep the compass point on A. Draw a small arc that cuts the line m at two points.
  2. Without changing the compass width, place the compass point on each cut point on m and draw two arcs on the other side of m so that they meet.
  3. The meeting point of these arcs is the image A′.
  4. Check: The line segment AA′ is perpendicular to m, and the line m is the midline of AA′.

Step 2: Reflect point B in line m

  1. Repeat the same steps for B to get its image B′.

Step 3: Reflect point C in line m

  1. Repeat the same steps for C to get its image C′.

Step 4: Join the points to make the two triangles

  1. Join A–B, B–C, and C–A to make triangle ABC.
  2. Join A′–B′, B′–C′, and C′–A′ to make triangle A′B′C′.

Step 5: Measure the sides

  • Measure AB, BC, CA.
  • Measure A′B′, B′C′, C′A′.

What do we observe?

The reflection (mirror image) in a line keeps distances the same. This means the length between any two original points is equal to the length between their images.

( AB = A′B′ )

( BC = B′C′ )

( CA = C′A′ )

Why is this true? (Idea)

A reflection in a line is an isometry (a distance-preserving transformation). The line m acts like a mirror. Each point and its image are on opposite sides of m, the segment joining them is perpendicular to m, and m cuts that segment exactly in the middle. So all side lengths stay the same after reflection.

Final Answer

Yes, Yes, Yes. We find that:

( AB = A′B′ )

( BC = B′C′ )

( CA = C′A′ )

Open NCERT PDF