What is a Triangle?

A triangle is one of the simplest and most important shapes in geometry. You see triangles in roof tops, road signboards, pieces of pizza, and many other objects around you. Even though it looks simple, a triangle has many interesting properties that we use in mathematics, science and even in real-life constructions.

In this topic, we focus only on what a triangle is and how we represent it in geometry, in a clear and student-friendly way.

Informally, you can think of a triangle as a three-sided closed shape. If you (i) take three sticks as shown in the following figrue and (ii) join their ends one by one, and (iii) finally reach back to the starting point without leaving any gaps, you get a triangle-like shape.

This closed shape has:

• three corners,
• three sides,
• and three angles.

So we often describe a triangle as a three-sided polygon.

In geometry, we can define a triangle more carefully:

Definition: A triangle is a closed figure formed by three line segments such that each segment meets the other two at its endpoints.

If the three corners are named \( A \), \( B \) and \( C \), we call the triangle triangle \( ABC \) and write it as \( \triangle ABC \).

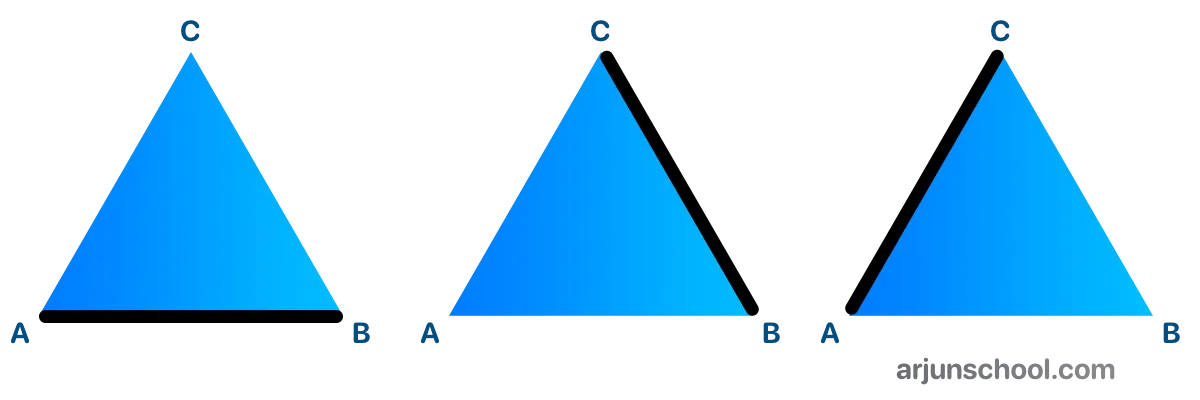
Here, the three line segments are \( \overline{AB} \), \( \overline{BC} \) and \( \overline{CA} \). These three segments together form the boundary of the triangle.

Without going into too much detail, we can quickly note the main parts that appear in every triangle:

• The corners of a triangle are called its vertices. In \( \triangle ABC \), the vertices are \( A \), \( B \) and \( C \).
• The line segments that join these vertices are called the sides of the triangle: \( \overline{AB} \), \( \overline{BC} \) and \( \overline{CA} \).
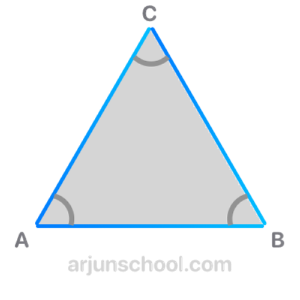
• The angles of the triangle are formed at each vertex: \( \angle A \), \( \angle B \) and \( \angle C \).

We will study these parts (sides, angles, special lines, etc.) in more detail in separate topics, but for now it is enough to know that every triangle naturally has three vertices, three sides and three angles.

To draw a triangle, we usually follow these steps:

1. Mark three points that are not in a straight line, say \( A \), \( B \) and \( C \).
2. Join them using straight line segments: \( \overline{AB} \), \( \overline{BC} \) and \( \overline{CA} \).

Once joined, the figure becomes triangle \( ABC \). We write it as \( \triangle ABC \), reading it as “triangle A B C”.

The order of letters \( A, B, C \) is usually chosen to follow the boundary of the triangle in one continuous direction (clockwise or anti-clockwise).

To form a proper triangle, the three points must not all lie on the same straight line. If they did, the three line segments would lie on that line and could not form a closed shape.

Important idea: A triangle is formed only when the three points are non-collinear (not on the same straight line). When this happens, joining them pairwise with line segments produces a closed three-sided figure, which is a triangle.

Triangles are not just textbook figures; they appear in many real-life designs because they are strong and stable shapes:

• Bridges and towers: Support structures often use triangular frames because triangles do not change shape easily when force is applied.
• Roof trusses: The frames supporting many roofs are made up of multiple triangles.
• Signboards and stands: Many stands and frames use triangular supports to balance weight.
• Art and patterns: Triangles are commonly used in designs, patterns and logos.

Seeing triangles in different objects around you helps you remember that a triangle is simply a three-sided closed figure made by three line segments.