1. Introduction to Naming a Triangle
In geometry, triangles are named in a consistent and meaningful way so that diagrams and explanations become easy to read. A triangle is usually named using its three vertices. The order in which we write the vertices determines how we move around the boundary of the triangle.
This topic explains how to correctly name triangles, their sides, and their angles.
2. Naming a Triangle Using Vertices
A triangle is named by listing its vertices in sequence. If the vertices are \( A \), \( B \), and \( C \), we name the triangle as triangle \( ABC \) and write it as \( \triangle ABC \).
The order of letters shows how we move around the triangle (clockwise or anti-clockwise). The same triangle can also be named as \( \triangle BCA \) or \( \triangle CAB \), because the order still goes around the boundary.
3. Naming Sides of a Triangle
The sides of a triangle are named using the endpoints of each side. For \( \triangle ABC \), the three sides are:
- \( \overline{AB} \)
- \( \overline{BC} \)
- \( \overline{CA} \)
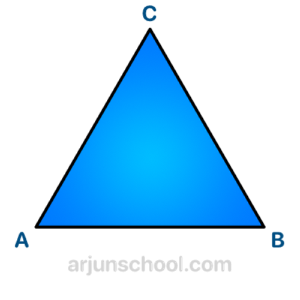
Each side lies opposite a vertex:
- Side \( \overline{BC} \) is opposite vertex \( A \)
- Side \( \overline{CA} \) is opposite vertex \( B \)
- Side \( \overline{AB} \) is opposite vertex \( C \)
3.1. Using Lowercase Letters for Sides
We often name sides using lowercase letters corresponding to the opposite vertex:
- Side opposite \( A \) is named \( a \)
- Side opposite \( B \) is named \( b \)
- Side opposite \( C \) is named \( c \)
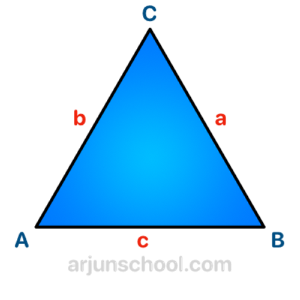
This notation is especially useful in formulas like the area of a triangle using Heron’s formula and in trigonometry.
4. Naming Angles of a Triangle
Angles in a triangle are named using three letters, with the vertex in the middle. In \( \triangle ABC \):
- \( \angle A = \angle BAC \)
- \( \angle B = \angle ABC \)
- \( \angle C = \angle ACB \)
Angles may sometimes be written with a single letter, like \( \angle A \), but this is done only when the angle is clear in the diagram.
4.1. Arms and Vertex Notation
The angle \( \angle ABC \) has:
- Vertex at \( B \)
- Arms along \( \overline{BA} \) and \( \overline{BC} \)
This helps avoid confusion when multiple angles meet at the same point.
5. Symbols and Notations Used for Triangles
In triangle notation, we use the following symbols:
- Triangle: \( \triangle ABC \)
- Sides: \( \overline{AB}, \overline{BC}, \overline{CA} \)
- Angles: \( \angle A, \angle B, \angle C \)
- Length of side: written as \( AB, BC, CA \)
Notice the difference: the symbol \( \overline{AB} \) represents the segment, while \( AB \) written without the bar means the length of the segment.
6. Understanding Order and Orientation
When naming a triangle, the order of letters must follow the boundary of the triangle. For example, \( \triangle ABC \) is valid, but \( \triangle ACB \) would mean tracing a different path.
As long as we move around the triangle in one continuous direction (clockwise or anti-clockwise), the naming is correct.
Incorrect naming—where the sequence jumps across the shape—can lead to confusion in geometry proofs and constructions.
7. Why Naming Matters
Clear naming helps us:
- identify sides and angles correctly,
- apply formulas accurately,
- communicate diagrams clearly,
- understand proofs step by step.
Once you are comfortable with naming and notation, the rest of triangle geometry becomes much easier to follow.