1. What is a Scalene Triangle?
A scalene triangle is a triangle in which all three sides are of different lengths. Because the sides are all unequal, the three interior angles are also different from one another.
This makes the scalene triangle the most general and irregular type of triangle.
2. Definition of a Scalene Triangle
Definition: A triangle is called a scalene triangle if none of its sides are equal in length. In symbolic form, for a triangle with sides \( a \), \( b \), and \( c \):
\( a \neq b, \ b \neq c, \ c \neq a \)
Because no sides are equal, the three angles are also never equal.
3. Properties of a Scalene Triangle
- All three sides have different lengths.
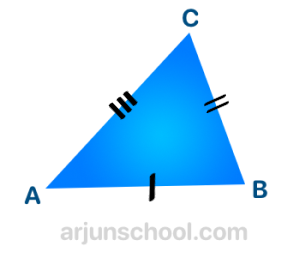
- All three angles have different measures.

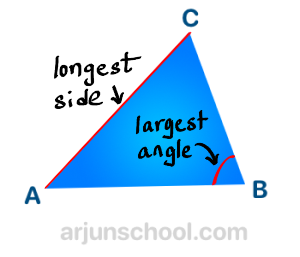
- The largest angle is opposite the longest side.
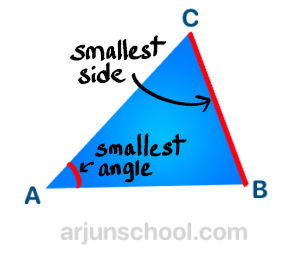
- The smallest angle is opposite the shortest side.
- It has no lines of symmetry.
3.1. Angles and Sides Relationship
In any scalene triangle, the angle–side relationship holds strongly:
- If \( a > b \), then \( \angle A > \angle B \)
- If \( b > c \), then \( \angle B > \angle C \)
Each angle reflects the length of the side opposite to it.
4. Examples of Scalene Triangles
Scalene triangles appear frequently in real life because objects and structures rarely have perfect symmetry.
- A triangular piece of land with irregular boundaries.
- A slice of pizza cut unevenly.
- Side view of a roof that is not the same on both sides.
- Any drawn triangle where no sides are intentionally made equal.
5. Scalene Triangle in Geometry Problems
Scalene triangles are used when a triangle does not have any special equality conditions. Many geometry problems assume a general triangle is scalene unless stated otherwise. Because of the unequal nature, you cannot directly use properties of isosceles or equilateral triangles.
In proofs and constructions, the scalene triangle helps show the most general case since no special sides or angles are equal.