NCERT Exemplar Solutions
Class 6 - Mathematics - Unit 9: Symmetry and Practical Geometry - Problems and SolutionsQuestion 74
Class 6 - Mathematics - Unit 9: Symmetry and Practical Geometry - Problems and Solutions
Question. 74
Complete Fig. 9.19 by taking l as the line of symmetry of the whole figure.
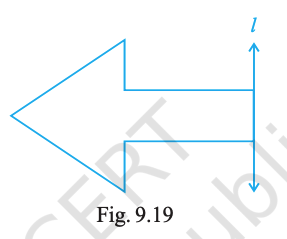
Answer:
Draw the mirror image of the given half across the line l to complete the symmetric figure.
Detailed Answer with Explanation:
Step-by-step (Beginner Friendly)
- Understand the goal
We want the whole figure to look the same on both sides of the line l. The line l is the mirror.
\(\text{line } l = \text{axis of symmetry}\)
- Pick a corner (vertex)
Choose any visible corner point on the given half. We will copy this point to the other side of l.
- Drop a perpendicular to the line
From the chosen point, draw a short line to l that meets l at a right angle.
\(\overline{PA} \perp l\)
\(\angle PAl = 90^\circ\)
- Measure the distance to the line
Note how far the point is from the line l along this perpendicular.
\(d = \text{distance}(P,\ l)\)
- Mark the mirror point on the other side
On the same perpendicular, mark a point at the same distance on the other side of l.
\(\text{If } \overline{PA} = d, \text{ then choose } P' \text{ on the other side with } \overline{AP'} = d\)
\(\Rightarrow P' \text{ is the reflection of } P \text{ in } l\)
- Repeat for all corners
Do the same perpendicular-and-equal-distance process for every vertex on the given half.
- Join the reflected points
Connect the new points in the same order as the original half (straight lines with straight lines, curves with curves) to complete the figure.
Quick Checks
- Each original point and its mirror point should be equally far from l.
- The joining segment between a point and its mirror should be perpendicular to l.
- After joining all, the left and right parts should overlap if folded on l.
Why this works
Reflection in a line keeps the distance to that line the same and flips the point to the opposite side.
\(\text{If } P' = \text{Ref}_l(P), \text{ then } \overline{AP} = \overline{AP'} \text{ and } \overline{PP'} \perp l\)