NCERT Exemplar Solutions
Class 6 - Mathematics - Unit 9: Symmetry and Practical Geometry - Problems and Solutions
Question 81

Question. 81

Copy Fig. 9.21 on your notebook and draw a perpendicular from P to line m, using (i) set squares (ii) Protractor (iii) ruler and compasses. How many such perpendiculars are you able to draw?

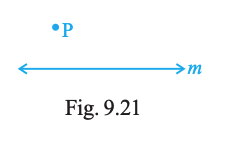
Answer:

One perpendicular.

Detailed Answer with Explanation:

Q81. Draw a perpendicular from point P to line m using (i) set squares (ii) protractor (iii) ruler & compasses. How many such perpendiculars can be drawn?

Key Idea (What is a perpendicular?)

Two lines are perpendicular if they meet to form a right angle.

( ext{Right angle} = 90^circ )

Method (i): Using Set Squares

  1. Place the longer edge of the set square along line m. Make sure it does not move.
  2. Keep a ruler (or another set square) pressed firmly against the short edge of your set square so the set square can slide along the ruler.
  3. Slide the set square along the ruler until one edge passes through point P.
  4. Draw the line through P along that edge. This line will meet m at a right angle.
  5. Mark the meeting point as X. Write the right-angle mark at X.

( angle PXM = 90^circ )

Method (ii): Using a Protractor

  1. Through point P, draw a light helper line that crosses line m. Mark the crossing point as X.
  2. Place the protractor at point X with the baseline along line m.
  3. From m, count to 90° on the protractor and make a small dot on that mark.
  4. Join point X to that dot to draw the 90° line.
  5. Extend this 90° line so that it passes through P (adjust your helper line if needed). This is the required perpendicular.

( ext{At } X: quad angle( ext{new line},, m) = 90^circ )

Method (iii): Using Ruler & Compasses

  1. Open the compass to a comfortable width (not too small). With center P, draw an arc that cuts line m at two points. Mark them as A and B.
  2. Keep the compass opening the same. With center A, draw a small arc below line m.
  3. With center B, draw another small arc (same opening) so it intersects the first arc. Mark the intersection as C.
  4. Draw the line PC. This line will meet m at a right angle.
  5. Mark the foot of the perpendicular as X where the line meets m.

Why this works: Points A and B are the same distance from X. Drawing equal arcs from A and B locates point C so that triangle AXB is isosceles and the line through the midpoint is a right angle.

( AX = BX )

( Rightarrow ) line through midpoint and vertex is perpendicular

( angle PXM = 90^circ )

Check Your Work

  • Use a set square or protractor at point X to verify the angle is 90°.
  • The shortest distance from P to line m is along the perpendicular. Your drawn line should look like the shortest path from P to m.

( ext{Shortest distance from a point to a line} = ext{perpendicular segment} )

Answer (How many perpendiculars?)

Only one perpendicular can be drawn from a point not on a line to that line.

This is a unique construction in Euclidean geometry.

( ext{From point } P otin m, exists! ext{line } PX perp m )

Open NCERT PDF
NCERT Exemplar Solutions Class 6 – Mathematics – Unit 9: Symmetry and Practical Geometry – Problems and Solutions | Detailed Answers