NCERT Exemplar Solutions
Class 6 - Mathematics - Unit 6: Mensuration - Multiple Choice QuestionsQuestion 1
Class 6 - Mathematics - Unit 6: Mensuration - Multiple Choice Questions
Question. 1
Following figures are formed by joining six unit squares. Which figure has the smallest perimeter in Fig. 6.4?
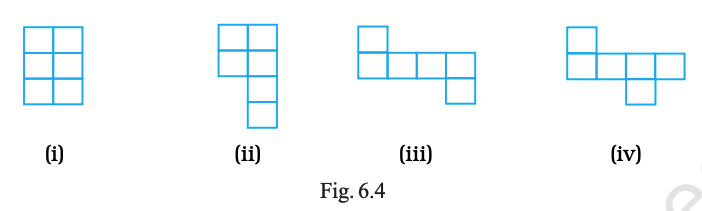
(ii)
(iii)
(iv)
(i)
Detailed Answer with Explanation:
Why (ii) has the smallest perimeter
Perimeter means the total length of the outer boundary.
Each unit square has 4 sides. For 6 unit squares, total sides before joining is:
\(4 \times 6 = 24\)
(This counts all sides, even the ones that will be shared inside.)
When two squares touch along a full side, that side is shared. A shared side is not on the outside, so it reduces the perimeter by 2 (because we counted it for both squares).
So, more shared sides ⇒ smaller perimeter.
Among the given figures, (ii) is the most compact: it is a 2 × 3 rectangle. Compact shapes have the maximum number of shared sides.
Count shared sides in the 2 × 3 rectangle:
Horizontal shares: 2 rows, each row has \(3 - 1 = 2\) shared sides.
So, \(2 \times 2 = 4\) shared sides.
Vertical shares: 3 columns, each column has \(2 - 1 = 1\) shared side.
So, \(3 \times 1 = 3\) shared sides.
Total shared sides = \(4 + 3 = 7\).
Now compute the perimeter:
Start with 24 sides.
Each shared side removes 2 from the perimeter count.
So, perimeter = \(24 - 2 \times 7\)
= \(24 - 14\)
= \(10\) units.
Any less compact shape (like (i), (iii), (iv)) has fewer shared sides, so its perimeter will be more than 10 units.
Therefore, figure (ii) (the 2 × 3 rectangle) has the smallest perimeter.