NCERT Exemplar Solutions
Class 6 - Mathematics - Unit 6: Mensuration - Problems and SolutionsQuestion 42
Class 6 - Mathematics - Unit 6: Mensuration - Problems and Solutions
Question. 42
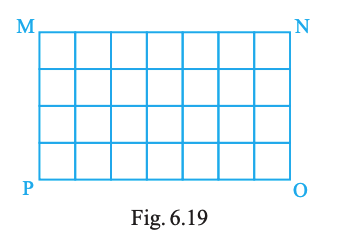
Rectangular wall MNOP of a kitchen is covered with square tiles of 15 cm length (Fig. 6.19). Find the area of the wall.
Answer:
Detailed Answer with Explanation:
Step 1: Understand one tile
Each tile is a square with side = (15 ext{cm}).
Area of 1 tile = (15 imes 15).
Compute: (15 imes 10 = 150), (15 imes 5 = 75).
So, (15 imes 15 = 150 + 75 = 225 ext{cm}^2).
Step 2: Count the tiles on the wall
From the figure, there are (9) tiles along the length and (5) tiles along the height.
Total number of tiles = (9 imes 5 = 45).
Step 3: Area of the whole wall
Total area = (number of tiles) ( imes) (area of 1 tile).
= (45 imes 225 ext{cm}^2).
Break it up: (225 imes 40 = 9000), (225 imes 5 = 1125).
Add: (9000 + 1125 = 10125 ext{cm}^2).
Answer: (10125 ext{cm}^2).
Why this works: Tiles exactly cover the wall without gaps or overlaps, so the wall’s area is just the sum of all tile areas.