NCERT Exemplar Solutions
Class 6 - Mathematics - Unit 8: Ratio & ProportionProblems and Solutions
Class 6 - Mathematics - Unit 8: Ratio & Proportion
Question. 47
The marked price of a table is Rs 625 and its sale price is Rs 500. What is the ratio of the sale price to the marked price?
Answer:
Ratio = 4 : 5
Open
Question. 48
Which pair of ratios are equal? And why?
(i) 2/3, 4/6
(ii) 8/4, 2/1
(iii) 4/5, 12/20
Answer:
(i) and (ii)
Open
Question. 50
Reshma prepared 18 kg of Burfi by mixing Khoya with sugar in the ratio of 7 : 2. How much Khoya did she use?
Answer:
14 kg
Open
Question. 51
A line segment 56 cm long is to be divided into two parts in the ratio of 2 : 5. Find the length of each part.
Answer:
16 cm and 40 cm
Open
Question. 52
The number of milk teeth in human beings is 20 and the number of permanent teeth is 32. Find the ratio of the number of milk teeth to the number of permanent teeth.
Answer:
5 : 8
Open
Question. 53
Sex ratio is defined as the number of females per 1000 males in the population. Find the sex ratio if there are 3732 females per 4000 males in a town.
Answer:
933
Open
Question. 54
In a year, Ravi earns Rs 360000 and paid Rs 24000 as income tax. Find the ratio of his
(a) income to income tax.
(b) income tax to income after paying income tax.
Answer:
(a) 15 : 1
(b) 1 : 14
Open
Question. 55
Ramesh earns Rs 28000 per month. His wife Rama earns Rs 36000 per month. Find the ratio of
(a) Ramesh’s earnings to their total earnings.
(b) Rama’s earnings to their total earnings.
Answer:
(a) 7 : 16
(b) 9 : 16
Open
Question. 56
Of the 288 persons working in a company, 112 are men and the remaining are women. Find the ratio of the number of
(a) men to that of women.
(b) men to the total number of persons.
(c) women to the total number of persons.
Answer:
(a) 7 : 11
(b) 7 : 18
(c) 11 : 18
Open
Question. 57
A rectangular sheet of paper is of length 1.2 m and width 21 cm. Find the ratio of width of the paper to its length.
Answer:
7 : 40
Open
Question. 58
A scooter travels 120 km in 3 hours and a train travels 120 km in 2 hours. Find the ratio of their speeds.
Answer:
2 : 3
Open
Question. 59
An office opens at 9 a.m. and closes at 5.30 p.m. with a lunch break of 30 minutes. What is the ratio of lunch break to the total period in the office?
Answer:
1 : 17
Open
Question. 60
The shadow of a 3 m long stick is 4 m long. At the same time of the day, if the shadow of a flagstaff is 24 m long, how tall is the flagstaff?
Answer:
18 m
Open
Question. 61
A recipe calls for 1 cup of milk for every 2½ cups of flour to make a cake that would feed 6 persons. How many cups of both flour and milk will be needed to make a similar cake for 8 people?
Answer:
4 2/3 cups
Open
Question. 62
In a school, the ratio of the number of large classrooms to small classrooms is 3 : 4. If the number of small rooms is 20, then find the number of large rooms.
Answer:
15
Open
Question. 63
Samira sells newspapers at Janpath crossing daily. On a particular day, she had 312 newspapers out of which 216 are in English and remaining in Hindi. Find the ratio of
(a) the number of English newspapers to the number of Hindi newspapers.
(b) the number of Hindi newspapers to the total number of newspapers.
Answer:
(a) 9 : 4
(b) 4 : 13
Open
Question. 64
The students of a school belong to different religious backgrounds. The number of Hindu students is 288, the number of Muslim students is 252, the number of Sikh students is 144 and the number of Christian students is 72. Find the ratio of
(a) the number of Hindu students to the number of Christian students.
(b) the number of Muslim students to the total number of students.
Answer:
(a) 4 : 1
(b) 1 : 3
Open
Question. 65
When Chinmay visited chowpati at Mumbai on a holiday, he observed that the ratio of North Indian food stalls to South Indian food stalls is 5 : 4. If the total number of food stalls is 117, find the number of each type of food stalls.
Answer:
65 North Indian and 52 South Indian food stalls
Open
Question. 66
At the parking stand of Ramleela ground, Kartik counted that there are 115 cycles, 75 scooters and 45 bikes. Find the ratio of the number of cycles to the total number of vehicles.
Answer:
23 : 47
Open
Question. 67
A train takes 2 hours to travel from Ajmer to Jaipur, which are 130 km apart. How much time will it take to travel from Delhi to Bhopal which are 780 km apart if the train is travelling at the uniform speed?
Answer:
12 hours
Open
Question. 68
The length and breadth of a school ground are 150 m and 90 m respectively, while the length and breadth of a mela ground are 210 m and 126 m, respectively. Are these measurements in proportion?
Answer:
Yes
Open
Question. 69
In Fig. 8.4, the comparative areas of the continents are given: What is the ratio of the areas of
(a) Africa to Europe
(b) Australia to Asia
(c) Antarctica to Combined area of North America and South America.

Answer:
(a) 13 : 5 (b) 2 : 11 (c) 13 : 35
Open
Question. 70
A tea merchant blends two varieties of tea costing her Rs 234 and Rs 130 per kg in the ratio of their costs. If the weight of the mixture is 84 kg, then find the weight of each variety of tea.
Answer:
54 kg and 30 kg
Open
Question. 71
An alloy contains only zinc and copper and they are in the ratio of 7 : 9. If the weight of the alloy is 8 kg, then find the weight of copper in the alloy.
Answer:
4\(\tfrac{1}{2}\) kg
Open
Question. 72
In the following figure, each division represents 1 cm: Express numerically the ratios of the following distances:
(i) AC : AF (ii) AG : AD (iii) BF : AI (iv) CE : DI

Answer:
(i) 2 : 5 (ii) 2 : 1 (iii) 1 : 2 (iv) 2 : 5
Open
Question. 73
Find two numbers whose sum is 100 and whose ratio is 9 : 16.
Answer:
73.36 and 64
Open
Question. 74
In Fig. 8.6 (i) and Fig. 8.6 (ii), find the ratio of the area of the shaded portion to that of the whole figure:

Answer:
1 : 2, 1 : 2
Open
Question. 75
A typist has to type a manuscript of 40 pages. She has typed 30 pages of the manuscript. What is the ratio of the number of pages typed to the number of pages left?
Answer:
3 : 1
Open
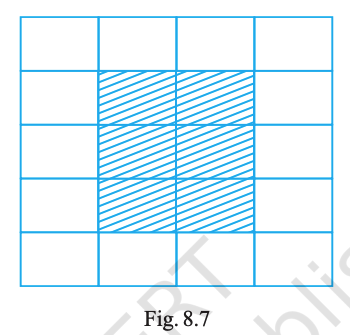
Question. 76
In a floral design made from tiles each of dimensions 40 cm by 60 cm (See Fig. 8.7), find the ratios of:
(a) the perimeter of shaded portion to the perimeter of the whole design.
(b) the area of the shaded portion to the area of the unshaded portion.
Answer:
(a) 5 : 9 (b) 3 : 10
Open
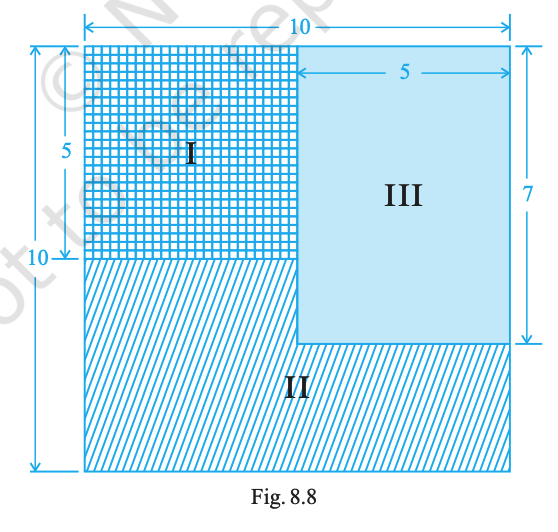
Question. 77
In Fig. 8.8, what is the ratio of the areas of
(a) shaded portion I to shaded portion II?
(b) shaded portion II to shaded portion III?
(c) shaded portions I and II taken together and shaded portion III?
Answer:
(a) 5 : 8 (b) 8 : 7 (c) 13 : 7
Open
Question. 78
A car can travel 240 km in 15 litres of petrol. How much distance will it travel in 25 litres of petrol?
Answer:
400 km
Open
Question. 79
Bachhu Manjhi earns Rs 24000 in 8 months. At this rate,
(a) how much does he earn in one year?
(b) in how many months does he earn Rs 42000?
Answer:
(a) Rs 36000
(b) 14 months
Open
Question. 80
The yield of wheat from 8 hectares of land is 360 quintals. Find the number of hectares of land required for a yield of 540 quintals?
Answer:
12 hectares
Open
Question. 81
The earth rotates 360° about its axis in about 24 hours. By how much degree will it rotate in 2 hours?
Answer:
30°
Open
Question. 82
Shivangi is suffering from anaemia as haemoglobin level in her blood is lower than the normal range. Doctor advised her to take one iron tablet two times a day. If the cost of 10 tablets is Rs 17, then what amount will she be required to pay for her medical bill for 15 days?
Answer:
Rs 51
Open
Question. 83
The quarterly school fee in Kendriya Vidyalaya for Class VI is Rs 540. What will be the fee for seven months?
Answer:
Rs 1260
Open
Question. 84
In an election, the votes cast for two of the candidates were in the ratio 5 : 7. If the successful candidate received 20734 votes, how many votes did his opponent receive?
Answer:
14810
Open
Question. 85
A metal pipe 3 metre long was found to weigh 7.6 kg. What would be the weight of the same kind of 7.8 m long pipe?
Answer:
19.76 kg
Open
Question. 86
A recipe for raspberry jelly calls for 5 cups of raspberry juice and 2\(\tfrac{1}{2}\) cups of sugar. Find the amount of sugar needed for 6 cups of the juice?
Answer:
3 cups
Open
Question. 87
A farmer planted 1890 tomato plants in a field in rows each having 63 plants. A certain type of worm destroyed 18 plants in each row. How many plants did the worm destroy in the whole field?
Answer:
540
Open
Question. 88
Length and breadth of the floor of a room are 5 m and 3 m, respectively. Forty tiles, each with area \(\tfrac{1}{16}\,\text{m}^2\), are used to cover the floor partially. Find the ratio of the tiled and the non tiled portion of the floor.
Answer:
1 : 5
Open
Question. 89
A carpenter had a board which measured 3 m × 2 m. She cut out a rectangular piece of 250 cm × 90 cm. What is the ratio of the area of cut out piece and the remaining piece?
Answer:
3 : 5