NCERT Solutions
Class 10 - Mathematics - Chapter 5: ARITHMETIC PROGRESSIONS - Exercise 5.3Question 18
Class 10 - Mathematics - Chapter 5: ARITHMETIC PROGRESSIONS - Exercise 5.3
Question. 18
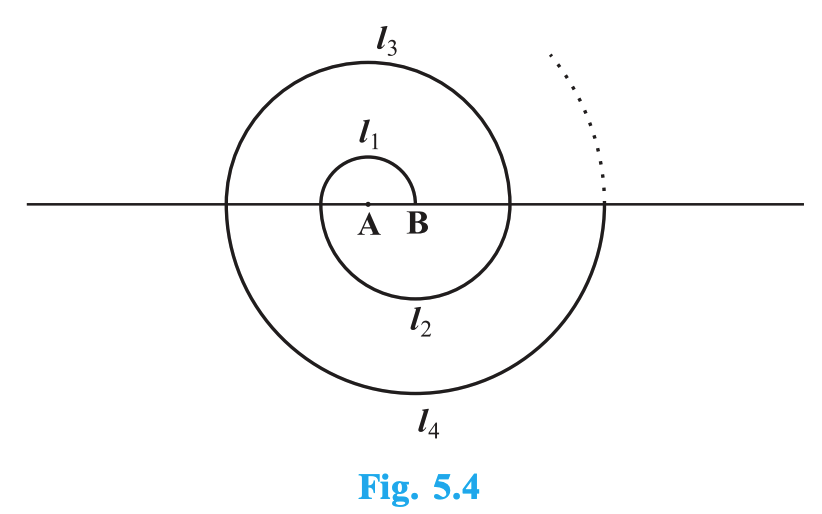
A spiral is made up of successive semicircles, with centres alternately at A and B, starting with centre at A, of radii 0.5 cm, 1.0 cm, 1.5 cm, 2.0 cm, . . . as shown in Fig. 5.4. What is the total length of such a spiral made up of thirteen consecutive semicircles? (Take \(\pi = \dfrac{22}{7}\))
Answer:
\(143\text{ cm}\)
Detailed Answer with Explanation:
Idea: The spiral is formed by joining semicircles. The length of each semicircle is half the circumference of a full circle, i.e. \(\text{length} = \pi r\). Add these lengths for all 13 semicircles.
Step 1: List the radii as an AP
The radii given are:
\[0.5\ \text{cm},\ 1.0\ \text{cm},\ 1.5\ \text{cm},\ 2.0\ \text{cm},\ \ldots\]
This is an arithmetic progression (AP) with:
First term \(a = 0.5\ \text{cm}\)
Common difference \(d = 0.5\ \text{cm}\)
Number of semicircles \(n = 13\).
The nth radius is:
\[r_n = a + (n - 1)d = 0.5 + (n - 1)\cdot 0.5 = 0.5n\]
So the radii for 13 semicircles are:
\[r_1 = 0.5,\ r_2 = 1.0,\ r_3 = 1.5,\ \ldots,\ r_{13} = 0.5 \cdot 13 = 6.5\ \text{cm}\]
Step 2: Length of one semicircle
Circumference of a full circle of radius \(r\) is \(2\pi r\).
Length of a semicircle (half circle) is:
\[L = \frac{1}{2} \cdot 2\pi r = \pi r\]
So each semicircle of radius \(r_i\) has length \(\pi r_i\).
Step 3: Total length of 13 semicircles
Total length \(L_T\) is:
\[L_T = \pi(r_1 + r_2 + \cdots + r_{13})\]
We must find the sum of all radii.
Since \(r_n = 0.5n\), the sum of radii is:
\[r_1 + r_2 + \cdots + r_{13} = 0.5(1 + 2 + 3 + \cdots + 13)\]
Now,
\[1 + 2 + 3 + \cdots + 13 = \frac{13 \cdot 14}{2} = 91\]
So,
\[r_1 + r_2 + \cdots + r_{13} = 0.5 \times 91 = \frac{91}{2} = 45.5\ \text{cm}\]
Therefore,
\[L_T = \pi \times 45.5\]
Step 4: Substitute \(\pi = \dfrac{22}{7}\)
\[L_T = \frac{22}{7} \times \frac{91}{2}\]
Simplify step by step:
\[\frac{22}{7} \times \frac{91}{2} = \frac{22 \times 91}{14}\]
Now, \(\dfrac{91}{7} = 13\), so:
\[\frac{22 \times 91}{14} = \frac{22 \times 13}{2} = \frac{286}{2} = 143\]
Conclusion: The total length of the spiral formed by thirteen semicircles is \(143\text{ cm}\).