NCERT Solutions
Class 10 - Mathematics - Chapter 5: ARITHMETIC PROGRESSIONS - Exercise 5.3Question 20
Class 10 - Mathematics - Chapter 5: ARITHMETIC PROGRESSIONS - Exercise 5.3
Question. 20
In a potato race, a bucket is placed at the starting point. The first potato is 5 m away, and each subsequent potato is 3 m apart in a straight line. There are ten potatoes. A competitor picks each potato one at a time, returns to the bucket, and continues. Find the total distance the competitor runs.
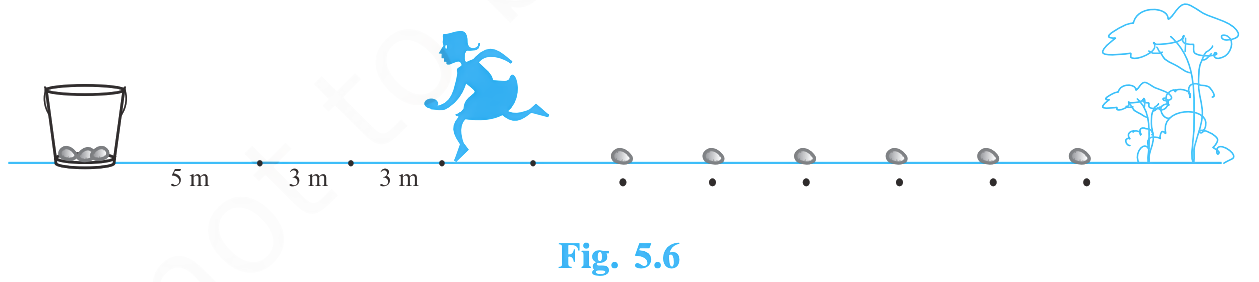
Answer:
\(370\text{ m}\)
Detailed Answer with Explanation:
Idea: For each potato, the competitor runs from the bucket to the potato and back to the bucket. So, if a potato is at distance \(d\) metres, the distance run for that potato is \(2d\) metres. We add this for all 10 potatoes.
Step 1: Write the distances of the potatoes from the bucket
The first potato is 5 m away. Each next potato is 3 m further than the previous one.
So the distances form an AP:
\[5, 8, 11, 14, \ldots\]
Here, first term \(a = 5\), common difference \(d = 3\), and number of potatoes \(n = 10\).
Step 2: Find the sum of distances to all potatoes
Sum of first \(n\) terms of an AP:
\[S_n = \frac{n}{2}[2a + (n - 1)d]\]
For \(n = 10\), \(a = 5\), \(d = 3\):
\[S_{10} = \frac{10}{2}[2 \cdot 5 + 9 \cdot 3]\]
\[S_{10} = 5[10 + 27] = 5 \cdot 37 = 185\]
So, the sum of all one-way distances to the potatoes is 185 m.
Step 3: Account for going and coming back
For each potato, the competitor goes to the potato and comes back to the bucket. So the distance for each potato is doubled.
Total distance run:
\[\text{Total distance} = 2 \times S_{10} = 2 \times 185 = 370\ \text{m}\]
Conclusion
The competitor runs a total distance of \(370\text{ m}\).