NCERT Solutions
Class 10 - Mathematics - Chapter 5: ARITHMETIC PROGRESSIONS - Exercise 5.4 (Optional)Question 5
Class 10 - Mathematics - Chapter 5: ARITHMETIC PROGRESSIONS - Exercise 5.4 (Optional)
Question. 5
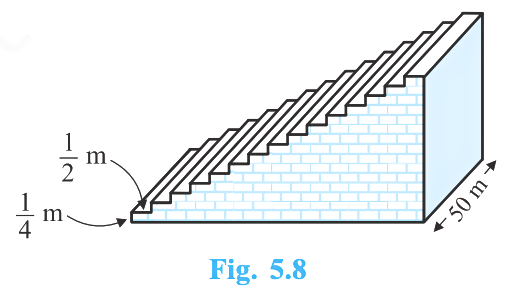
A small terrace at a football ground comprises of 15 steps each of which is 50 m long and built of solid concrete. Each step has a rise of \(\dfrac{1}{4}\) m and a tread of \(\dfrac{1}{2}\) m (see Fig. 5.8). Calculate the total volume of concrete required to build the terrace.
Hint: Volume of concrete required to build the first step \(= \dfrac{1}{4} \times \dfrac{1}{2} \times 50\,\text{m}^3\).
Answer:
\(750\,\text{m}^3\)
Detailed Answer with Explanation:
Step 1: Understand the shape of each step.
Each step is like a solid rectangular block with:
- Length (along the terrace) = 50 m
- Rise (height) = \(\dfrac{1}{4}\) m
- Tread (depth) = \(\dfrac{1}{2}\) m
But as we go up, each new step extends one more tread further back than the one below it.
Step 2: Write the volume of each step.
For a rectangular block:
\[\text{Volume} = \text{length} \times \text{breadth} \times \text{height}\]
First step:
Depth = \(\dfrac{1}{2}\) m, height = \(\dfrac{1}{4}\) m, length = 50 m.
\[V_1 = 50 \times \dfrac{1}{2} \times \dfrac{1}{4} = 50 \times \dfrac{1}{8} = \dfrac{50}{8}\,\text{m}^3\]
Second step:
It occupies two treads in depth: \(2 \times \dfrac{1}{2} = 1\) m.
\[V_2 = 50 \times 1 \times \dfrac{1}{4} = 50 \times \dfrac{1}{4} = \dfrac{50}{4}\,\text{m}^3\]
Third step:
Depth = \(3 \times \dfrac{1}{2} = \dfrac{3}{2}\) m.
\[V_3 = 50 \times \dfrac{3}{2} \times \dfrac{1}{4} = 50 \times \dfrac{3}{8} = \dfrac{150}{8}\,\text{m}^3\]
Continuing in this way, the \(n\)th step has depth \(\dfrac{n}{2}\) m, so:
\[V_n = 50 \times \dfrac{n}{2} \times \dfrac{1}{4} = 50 \times \dfrac{n}{8} = \dfrac{50}{8}n = \dfrac{25}{4}n\,\text{m}^3\]
Step 3: Sum the volumes of all 15 steps.
We need:
\[V_{\text{total}} = V_1 + V_2 + \cdots + V_{15}\]
Using the formula for \(V_n\):
\[V_{\text{total}} = \sum_{n=1}^{15} \dfrac{25}{4}n = \dfrac{25}{4} \sum_{n=1}^{15} n\]
Now,
\[\sum_{n=1}^{15} n = \dfrac{15 \cdot 16}{2} = 120\]
So,
\[V_{\text{total}} = \dfrac{25}{4} \times 120 = 25 \times 30 = 750\,\text{m}^3\]
Conclusion
The total volume of concrete required to build the terrace is \(750\,\text{m}^3\).