NCERT Exemplar Solutions
Class 6 - Mathematics - Unit 2: Geometry - Fill in the BlanksQuestion 21
Class 6 - Mathematics - Unit 2: Geometry - Fill in the Blanks
Question. 21
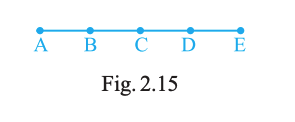
21. In Fig. 2.15, points A, B, C, D and E are collinear such that AB = BC = CD = DE. Then
(a) AD = AB + _____
(b) AD = AC + _____
(c) mid point of AE is _____
(d) mid point of CE is _____
(e) AE = _____ × AB
Answer:
(a) AD = AB + BC + CD
(b) AD = AC + CD
(c) Midpoint of AE is C
(d) Midpoint of CE is D
(e) AE = 4 × AB
Detailed Answer with Explanation:
All five points are on one straight line and the four small segments are equal:
Let
\[ AB = x \]
Then
\[ BC = x,\quad CD = x,\quad DE = x \]
Build longer segments from equal parts
\[ AC = AB + BC = x + x = 2x \]
\[ AD = AB + BC + CD = x + x + x = 3x \]
\[ AE = AB + BC + CD + DE = x + x + x + x = 4x \]
(a) From the diagram, going from A to D passes through B and C:
\[ AD = AB + BC + CD = AB + (\,\underline{BC + CD}\,) \]
(b) First reach C from A, then add one more equal part to reach D:
\[ AC = AB + BC = 2x \]
\[ AD = AC + CD = AC + (\,\underline{CD}\,) \]
(c) Midpoint of \(AE\):
\[ AE = 4x \Rightarrow \text{half of } AE = 2x \]
Starting at A, after two equal parts (\(AB\) then \(BC\)) we reach C.
So, the midpoint of \(AE\) is \(\underline{C}\).
(d) Midpoint of \(CE\):
\[ CE = CD + DE = x + x = 2x \Rightarrow \text{half of } CE = x \]
From C, one equal part (\(CD\)) takes us to D.
So, the midpoint of \(CE\) is \(\underline{D}\).
(e) Compare \(AE\) with \(AB\):
\[ AE = 4x = \underline{4}\times AB \]
Hence the filled answers follow directly from adding equal segments and identifying halfway points.