NCERT Exemplar Solutions
Class 6 - Mathematics - Unit 2: Geometry
Multiple Choice Questions

In each of the questions 1 to 16, out of four options only one is correct. Write the correct answer.

Quick Links to Questions

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

Question.  1

Number of lines passing through five points such that no three of them are collinear is

(A)

10

(B)

5

(C)

20

(D)

8

Detailed Step by Step Answer

Question.  2

The number of diagonals in a septagon is

(A)

21

(B)

42

(C)

7

(D)

14

Detailed Step by Step Answer

Question.  3

Number of line segments in Fig. 2.5 is

(A)

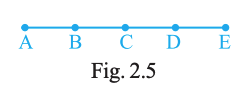
5

(B)

10

(C)

15

(D)

20

Detailed Step by Step Answer

Question.  4

Measures of the two angles between hour and minute hands of a clock at 9 O’clock are

(A)

60°, 300°

(B)

270°, 90°

(C)

75°, 285°

(D)

30°, 330°

Detailed Step by Step Answer

Question.  5

If a bicycle wheel has 48 spokes, then the angle between a pair of two consecutive spokes is

(A)

5\(\tfrac{1}{2}\)

(B)

7\(\tfrac{1}{2}\)

(C)

\(\tfrac{2}{11}\)

(D)

\(\tfrac{2}{15}\)

Detailed Step by Step Answer

Question.  6

In Fig. 2.6, \(\angle XYZ\) cannot be written as

(A)

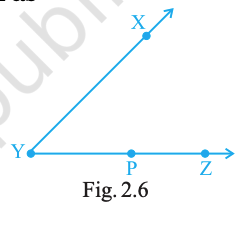
\(\angle Y\)

(B)

\(\angle ZXY\)

(C)

\(\angle ZYX\)

(D)

\(\angle XYP\)

Detailed Step by Step Answer

Question.  7

In Fig. 2.7, if point A is shifted to point B along the ray PX such that PB = 2PA, then the measure of \(\angle BPY\) is

(A)

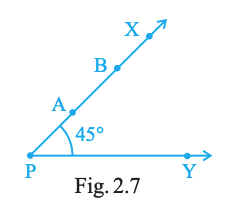
greater than 45°

(B)

45°

(C)

less than 45°

(D)

90°

Detailed Step by Step Answer

Question.  8

The number of angles in Fig. 2.8 is

(A)

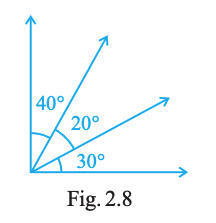
3

(B)

4

(C)

5

(D)

6

Detailed Step by Step Answer

Question.  9

The number of obtuse angles in Fig. 2.9 is

(A)

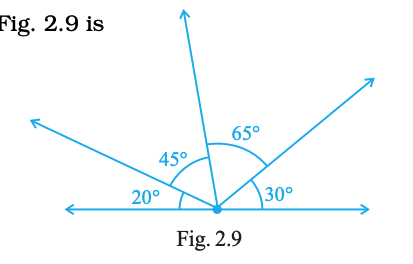
2

(B)

3

(C)

4

(D)

5

Detailed Step by Step Answer

Question.  10

The number of triangles in Fig. 2.10 is

(A)

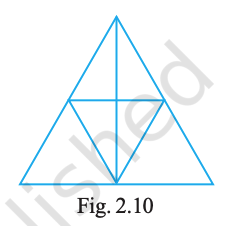
10

(B)

12

(C)

13

(D)

14

Detailed Step by Step Answer

Question.  11

If the sum of two angles is greater than 180°, then which of the following is not possible for the two angles?

(A)

One obtuse angle and one acute angle

(B)

One reflex angle and one acute angle

(C)

Two obtuse angles

(D)

Two right angles

Detailed Step by Step Answer

Question.  12

If the sum of two angles is equal to an obtuse angle, then which of the following is not possible?

(A)

One obtuse angle and one acute angle

(B)

One right angle and one acute angle

(C)

Two acute angles

(D)

Two right angles

Detailed Step by Step Answer

Question.  13

A polygon has prime number of sides. Its number of sides is equal to the sum of the two least consecutive primes. The number of diagonals of the polygon is

(A)

4

(B)

5

(C)

7

(D)

10

Detailed Step by Step Answer

Question.  14

In Fig. 2.11, AB = BC and AD = BD = DC. The number of isosceles triangles in the figure is

(A)

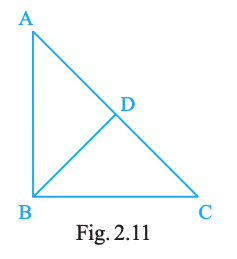
1

(B)

2

(C)

3

(D)

4

Detailed Step by Step Answer

Question.  15

In Fig. 2.12, \(\angle BAC = 90°\) and AD ⟂ BC. The number of right triangles in the figure is

(A)

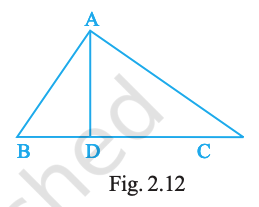
1

(B)

2

(C)

3

(D)

4

Detailed Step by Step Answer

Question.  16

In Fig. 2.13, PQ ⟂ RQ, PQ = 5 cm and QR = 5 cm. Then \(\triangle PQR\) is

(A)

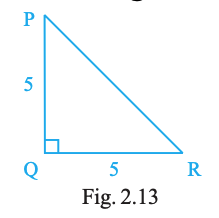
a right triangle but not isosceles

(B)

an isosceles right triangle

(C)

isosceles but not a right triangle

(D)

neither isosceles nor right triangle

Detailed Step by Step Answer
NCERT Exemplar Solutions Class 6 – Mathematics – Unit 2: Geometry – Multiple Choice Questions | Detailed Answers