NCERT Exemplar Solutions
Class 6 - Mathematics - Unit 2: Geometry - Multiple Choice Questions
Question 14

Question.  14

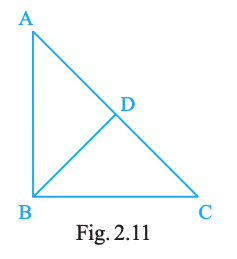
In Fig. 2.11, AB = BC and AD = BD = DC. The number of isosceles triangles in the figure is

(A)

1

(B)

2

(C)

3

(D)

4

Detailed Answer with Explanation:

Idea: Use the equal lengths to find triangles having two equal sides.

Step 1: From the figure, points A, B, C lie on one straight line.
So there is no triangle formed only by A, B, C. Hence, \(\triangle ABC\) does not exist.

Step 2: Note the given equalities, written one per line:

\(AB = BC\)

\(AD = BD\)

\(BD = CD\)

\(AD = CD\)

Step 3: Count isosceles triangles using point D.

  • \(\triangle ABD:\) here \(AD = BD\). So it is isosceles.
  • \(\triangle BCD:\) here \(BD = CD\). So it is isosceles.
  • \(\triangle ACD:\) here \(AD = CD\). So it is isosceles.

Step 4: Check if there are any others.
Any triangle not using D would need A, B, C, but they are collinear, so no triangle there.

Conclusion: Exactly 3 isosceles triangles: \(\triangle ABD,\ \triangle BCD,\ \triangle ACD\).
Answer: 3.

Open NCERT PDF
NCERT Exemplar Solutions Class 6 – Mathematics – Unit 2: Geometry – Multiple Choice Questions | Detailed Answers