NCERT Exemplar Solutions
Class 6 - Mathematics - Unit 2: GeometryProblems and Solutions
Class 6 - Mathematics - Unit 2: Geometry
Question. 42
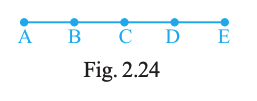
Name all the line segments in Fig. 2.24.
Answer:
AB, BC, CD, DE, AC, BD, CE, AD, BE, AE
Open
Question. 43
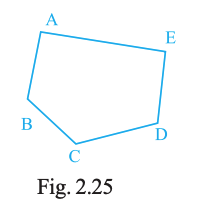
Name the line segments shown in Fig. 2.25.
Answer:
AB, BC, CD, DE, EA
Open
Question. 44
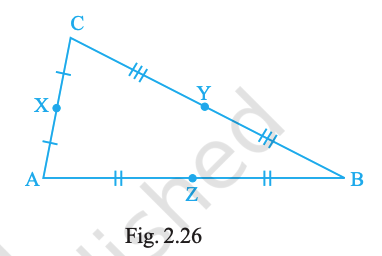
State the mid-points of all the sides of Fig. 2.26.
Answer:
Mid-point of \(AC\): X; mid-point of \(CB\): Y; mid-point of \(AB\): Z.
Open
Question. 45
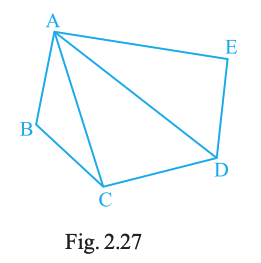
Name the vertices and the line segments in Fig. 2.27.
Answer:
Vertices: A, B, C, D, E.
Line segments: AB, BC, CD, DE, EA (sides), and diagonals AD, CE.
Open
Question. 46
Write down fifteen angles (less than \(180^{\circ}\)) involved in Fig. 2.28.
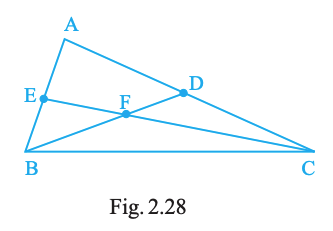
Answer:
One possible list (any equivalent 15 earns full credit):
∠ABC, ∠ABD, ∠ABE, ∠ABF, ∠CBD, ∠CBE, ∠CBF, ∠DBE, ∠DBF, ∠EBF, ∠BAC, ∠BAD, ∠BAE, ∠CAF, ∠DAF.
Open
Question. 47
Name the following angles of Fig. 2.29, using three letters:
(a) ∠1 (b) ∠2 (c) ∠3 (d) ∠1+∠2 (e) ∠2+∠3 (f) ∠1+∠2+∠3 (g) ∠CBA − ∠1
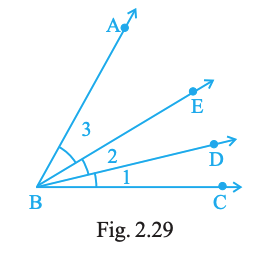
Answer:
(a) ∠CBD (b) ∠DBE (c) ∠EBA
(d) ∠CBE (e) ∠DBA (f) ∠CBA (g) ∠DBA
Open
Question. 48
Name the points and then the line segments in each of the following figures (Fig. 2.30).
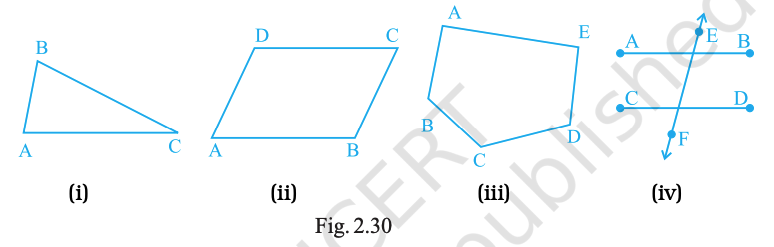
Answer:
(i) Points: A, B, C. Segments: AB, BC, CA.
(ii) Points: A, B, C, D. Segments: AB, BC, CD, DA.
(iii) Points: A, B, C, D, E. Segments: AB, BC, CD, DE, EA, AD.
(iv) Points: A, B, C, D, E, F. Segments: AB (shown as A–E–B in one line), EF (vertical), CD (horizontal).
Open
Question. 49
Which points in Fig. 2.31 appear to be mid-points of the line segments? When you locate a mid-point, name the two equal line segments formed by it.
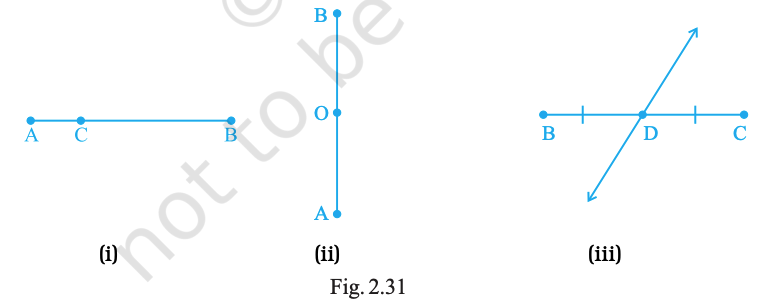
Answer:
(i) C is the mid-point of \(\overline{AB}\); segments: AC and CB.
(ii) O is the mid-point of \(\overline{AB}\); segments: AO and OB.
(iii) D is the mid-point of \(\overline{BC}\); segments: BD and DC.
Open
Question. 50
Is it possible for the same (a) line segment to have two different lengths? (b) angle to have two different measures?
Answer:
(a) No (b) No
Open
Question. 51
Will the measure of ∠ABC and of ∠CBD make measure of ∠ABD in Fig. 2.32?
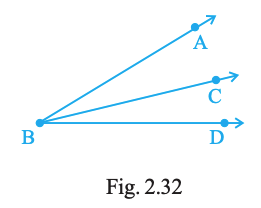
Answer:
Yes.
Open
Question. 52
Will the lengths of line segment AB and line segment BC make the length of line segment AC in Fig. 2.33?
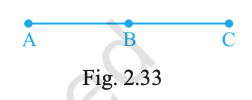
Answer:
Yes, since B lies between A and C, so \(AB+BC=AC\).
Open
Question. 53
Draw two acute angles and one obtuse angle without using a protractor. Estimate their measures; then check with a protractor.
Answer:
Example choices: draw roughly 35°, 60° (acute) and 120° (obtuse). After measuring, record actual values (e.g., 34°, 62°, 119°).
Open
Question. 54
Look at Fig. 2.34. Mark (a) a point A which is in the interior of both ∠1 and ∠2; (b) a point B which is in the interior of only ∠1; (c) a point C in the interior of ∠1. Now state whether points B and C lie in the interior of ∠2 also.
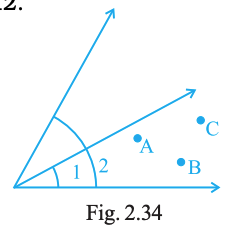
Answer:
One possible marking (as in the figure): A lies inside both ∠1 and ∠2; B lies inside only ∠1; C lies inside ∠1.
Thus, B is not in ∠2; C is not in ∠2.
Open
Question. 55
Find out the incorrect statement, if any, in the following: An angle is formed when we have (a) two rays with a common end-point (b) two line segments with a common end-point (c) a ray and a line segment with a common end-point
Answer:
Incorrect: (b) and (c)
Open
Question. 56
In which of the following figures (Fig. 2.35), (a) perpendicular bisector is shown? (b) bisector is shown? (c) only bisector is shown? (d) only perpendicular is shown?
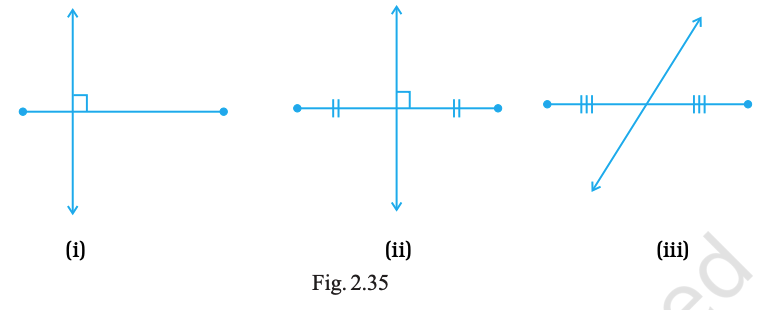
Answer:
(a) (ii)
(b) (ii) and (iii)
(c) (iii)
(d) (i)
Open
Question. 57
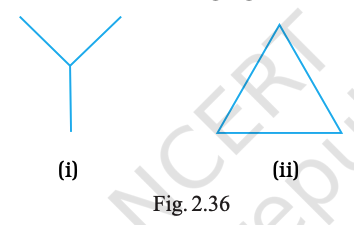
What is common in the following figures (i) and (ii) (Fig. 2.36)? Is Fig. 2.36(i) that of a triangle? If not, why?
Answer:
Common feature: both are formed by three line segments.
Fig. 2.36(i) is not a triangle because the three segments do not form a closed figure (their ends are not joined).
Open
Question. 58
If two rays intersect, will their point of intersection be the vertex of an angle of which the rays are the two sides?
Answer:
Yes.
Open
Question. 59
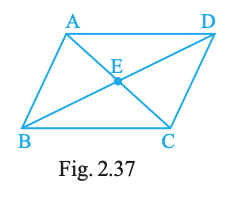
In Fig. 2.37, (a) name any four angles that appear to be acute angles. (b) name any two angles that appear to be obtuse angles.
Answer:
(a) Acute (any four): ∠AEB, ∠BEC, ∠CED, ∠DEA.
(b) Obtuse (any two): ∠ABC, ∠CDA.
Open
Question. 60
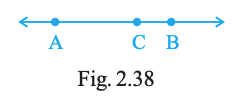
In Fig. 2.38, (a) is \(AC+CB=AB\)? (b) is \(AB+AC=CB\)? (c) is \(AB+BC=CA\)?
Answer:
(a) Yes (b) No (c) Yes
Question. 61
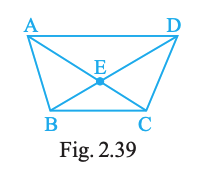
In Fig. 2.39, answer:
(a) What is AE + EC?
(b) What is AC − EC?
(c) What is BD − BE?
(d) What is BD − DE?
Answer:
(a) AC
(b) AE
(c) DE
(d) BE
Open
Question. 62
Using the information given, name the right angles in each part of Fig. 2.40.
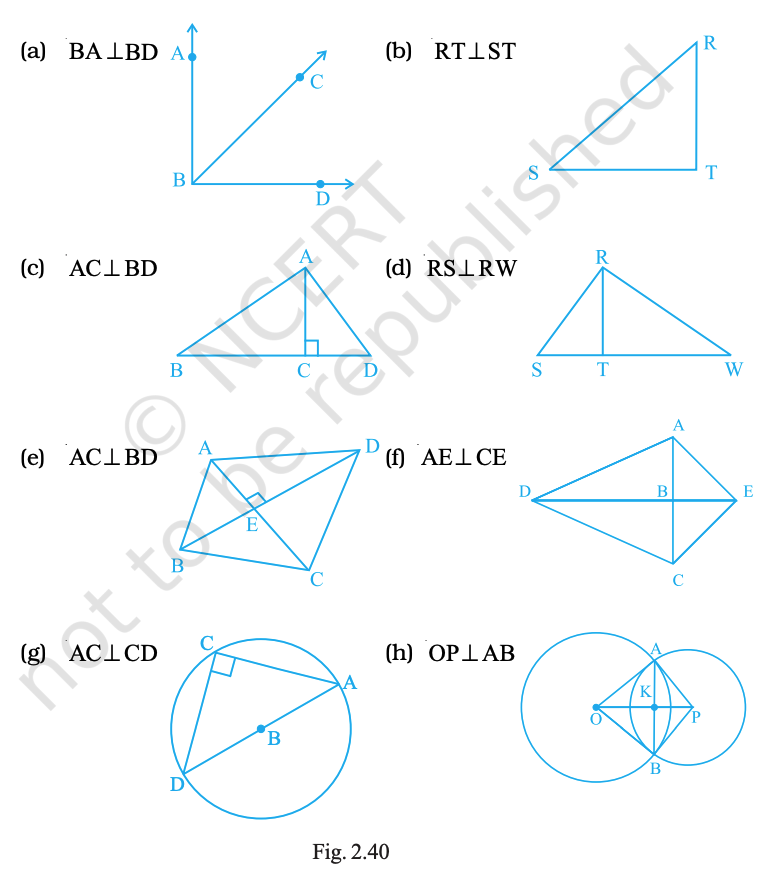
Answer:
(a) BA ⟂ BD ⇒ right angle: ∠ABD (at B).
(b) RT ⟂ ST ⇒ right angle: ∠RTS (at T).
(c) AC ⟂ BD ⇒ right angles at C: ∠ACB and ∠DCA.
(d) RS ⟂ RW ⇒ right angle: ∠SRW (at R).
(e) AC ⟂ BD (diagonals) ⇒ all four angles at E, e.g. ∠AEB, ∠BED, ∠DEC, ∠CEA, are right.
(f) AE ⟂ CE ⇒ right angle: ∠AEC.
(g) AC ⟂ CD ⇒ right angle: ∠ACD (at C).
(h) OP ⟂ AB (line of centres ⟂ common chord) ⇒ right angles at K (midpoint of AB): ∠OKA, ∠OKB, ∠PKA, ∠PKB.
Open
Question. 63
What conclusion can be drawn from each part of Fig. 2.41 if
(a) DB is the bisector of ∠ADC?
(b) BD bisects ∠ABC?
(c) DC is the bisector of ∠ADB, CA ⟂ DA and CB ⟂ DB?
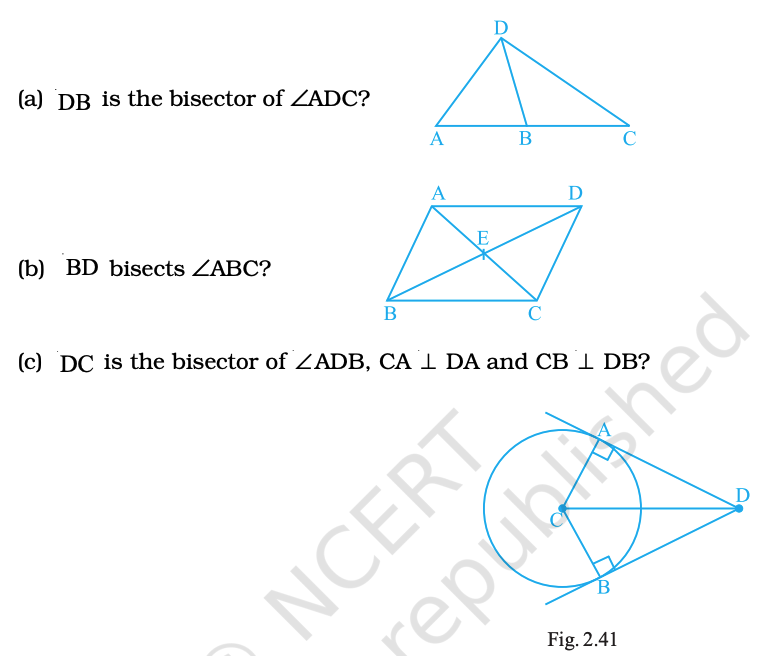
Answer:
(a) ∠ADB = ∠BDC.
(b) ∠ABD = ∠DBC.
(c) DA and DB are tangents to the circle at A and B respectively; the tangents from D are equal, so DA = DB, and the line from the centre CD bisects the angle between them.
Open
Question. 64
An angle is trisected if it is divided into three equal parts. If in Fig. 2.42, \(∠BAC = ∠CAD = ∠DAE\), how many trisectors are there for \(∠BAE\)?
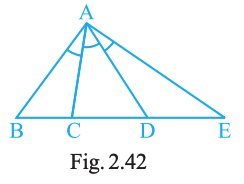
Answer:
Two — the rays AC and AD.
Open
Question. 65
How many points are marked in Fig. 2.43?
Answer:
2 — A and B.
Open
Question. 66
How many line segments are there in Fig. 2.43?
Answer:
1 — segment AB.
Open
Question. 67
In Fig. 2.44, how many points are marked? Name them.
Answer:
3 — A, B, C.
Open
Question. 68
How many line segments are there in Fig. 2.44? Name them.
Answer:
3 — AB, BC, AC.
Open
Question. 69
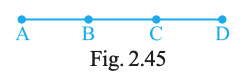
In Fig. 2.45 how many points are marked? Name them.
Answer:
4 — A, B, C, D.
Open
Question. 70
In Fig. 2.45 how many line segments are there? Name them.
Answer:
6 — AB, AC, AD, BC, BD, CD.
Open
Question. 71
In Fig. 2.46, how many points are marked? Name them.
Answer:
5 — A, B, D, E, C.
Open
Question. 72
In Fig. 2.46 how many line segments are there? Name them.
Answer:
10 — AB, AD, AE, AC, BD, BE, BC, DE, DC, EC.
Open
Question. 73
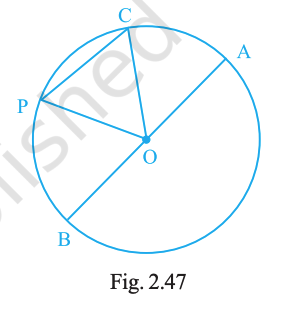
In Fig. 2.47, O is the centre of the circle.
(a) Name all chords of the circle.
(b) Name all radii of the circle.
(c) Name a chord which is not a diameter.
(d) Shade sectors OAC and OPB.
(e) Shade the smaller segment of the circle formed by CP.
Answer:
(a) Chords (joining any two points on the circle): AB, BC, CA, AP, PB, PC (of these, AP is a diameter).
(b) Radii: OA, OB, OC, OP.
(c) Example: PC (also AB, BC, CA, PB).
(d) Sector OAC is bounded by radii OA and OC and arc AC; sector OPB is bounded by OP and OB and arc PB.
(e) The smaller segment is the region bounded by chord CP and the minor arc CP.
Open
Question. 74
Can we have two acute angles whose sum is
(a) an acute angle? (b) a right angle? (c) an obtuse angle? (d) a straight angle? (e) a reflex angle?
Answer:
(a) Yes; e.g., \(20^{\circ}+30^{\circ}=50^{\circ}\) (acute).
(b) Yes; e.g., \(30^{\circ}+60^{\circ}=90^{\circ}\).
(c) Yes; e.g., \(50^{\circ}+60^{\circ}=110^{\circ}\) (obtuse).
(d) No; sum of two acute angles is \(<180^{\circ}\).
(e) No; a reflex angle is \(>180^{\circ}\), impossible with two acute angles.
Open
Question. 75
Can we have two obtuse angles whose sum is
(a) a reflex angle? (b) a complete angle?
Answer:
(a) Yes; e.g., \(100^{\circ}+110^{\circ}=210^{\circ}\) (reflex).
(b) No; each obtuse angle is \(>90^{\circ}\) and \(<180^{\circ}\), so their sum is \(>180^{\circ}\) but \(<360^{\circ}\); it can never be \(360^{\circ}\).
Open
Question. 76
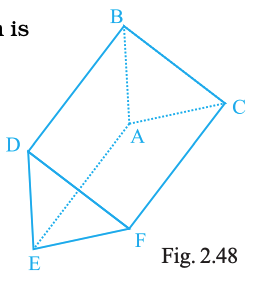
Write the name of (a) vertices, (b) edges, and (c) faces of the prism shown in Fig. 2.48.
Answer:
(a) Vertices: B, C, D, E, F (and the sixth corresponding vertex on the hidden back corner — the sketch labels only five explicitly).
(b) Edges (those shown): BC, CD, DB, EF, FD, DE, BE, CF, DF.
(c) Faces (those visible): triangular faces BCD and DEF; lateral quadrilaterals such as BEFC, CFDB, and BDE?E (back face).
Open
Question. 77
How many edges, faces and vertices are there in a sphere?
Answer:
Edges: 0, Faces: 1 curved surface, Vertices: 0.
Open
Question. 78
Draw all the diagonals of a pentagon ABCDE and name them.
Answer:
Diagonals are: AC, AD, BD, BE, CE.