NCERT Exemplar Solutions
Class 6 - Mathematics - Unit 2: Geometry - Problems and Solutions
Question 47

Question. 47

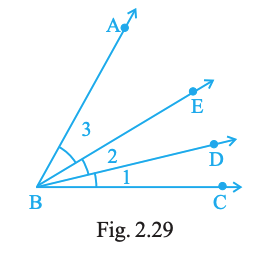
Name the following angles of Fig. 2.29, using three letters:

(a) ∠1   (b) ∠2   (c) ∠3   (d) ∠1+∠2   (e) ∠2+∠3   (f) ∠1+∠2+∠3   (g) ∠CBA − ∠1

Answer:

(a) ∠CBD   (b) ∠DBE   (c) ∠EBA

(d) ∠CBE   (e) ∠DBA   (f) ∠CBA   (g) ∠DBA

Detailed Answer with Explanation:

Key idea: To name an angle with three letters, the middle letter is the vertex. Here, the vertex is B. The first and last letters sit on the two arms forming the angle.

  • (a) \(\angle 1\):

    Arms used: \(\overrightarrow{BC}\) and \(\overrightarrow{BD}\).

    Start on \(C\), vertex at \(B\), end at \(D\): \(\angle \mathbf{CBD}\).

  • (b) \(\angle 2\):

    Arms used: \(\overrightarrow{BD}\) and \(\overrightarrow{BE}\).

    Start on \(D\), vertex at \(B\), end at \(E\): \(\angle \mathbf{DBE}\).

  • (c) \(\angle 3\):

    Arms used: \(\overrightarrow{BE}\) and \(\overrightarrow{BA}\).

    Start on \(E\), vertex at \(B\), end at \(A\): \(\angle \mathbf{EBA}\).

  • (d) \(\angle 1 + \angle 2\):

    Combine (a) and (b): from \(\overrightarrow{BC}\) to \(\overrightarrow{BE}\) passing through \(\overrightarrow{BD}\).

    Start on \(C\), vertex at \(B\), end at \(E\): \(\angle \mathbf{CBE}\).

  • (e) \(\angle 2 + \angle 3\):

    Combine (b) and (c): from \(\overrightarrow{BD}\) to \(\overrightarrow{BA}\) passing through \(\overrightarrow{BE}\).

    Start on \(D\), vertex at \(B\), end at \(A\): \(\angle \mathbf{DBA}\).

  • (f) \(\angle 1 + \angle 2 + \angle 3\):

    Combine all three: from \(\overrightarrow{BC}\) to \(\overrightarrow{BA}\).

    Start on \(C\), vertex at \(B\), end at \(A\): \(\angle \mathbf{CBA}\).

  • (g) \(\angle CBA - \angle 1\):

    Whole \(\angle CBA\) is from \(\overrightarrow{BC}\) to \(\overrightarrow{BA}\).

    Subtract \(\angle 1\) (from \(\overrightarrow{BC}\) to \(\overrightarrow{BD}\)).

    Remaining part: from \(\overrightarrow{BD}\) to \(\overrightarrow{BA}\) = \(\angle \mathbf{DBA}\).

Notes: The vertex letter B must stay in the middle. Sums of adjacent angles “extend” across the common arm. Subtraction removes the smaller adjacent part from the larger angle.

Open NCERT PDF