NCERT Exemplar Solutions
Class 6 - Mathematics - Unit 2: Geometry - Problems and SolutionsQuestion 46
Class 6 - Mathematics - Unit 2: Geometry - Problems and Solutions
Question. 46
Write down fifteen angles (less than \(180^{\circ}\)) involved in Fig. 2.28.
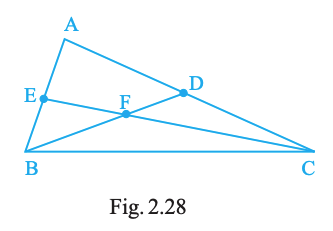
Answer:
One possible list (any equivalent 15 earns full credit):
∠ABC, ∠ABD, ∠ABE, ∠ABF, ∠CBD, ∠CBE, ∠CBF, ∠DBE, ∠DBF, ∠EBF, ∠BAC, ∠BAD, ∠BAE, ∠CAF, ∠DAF.
Detailed Answer with Explanation:
Idea: An angle is made by two rays starting from the same point (the vertex).
We will list angles that are clearly less than \(180^{\circ}\). These are called minor angles.
-
Read rays at vertex \(B\):
Rays from \(B\): \(BA\), \(BC\), \(BD\), \(BE\), \(BF\).
Form angles by taking pairs of these rays and choosing the smaller turn.
-
Angles at \(B\) using ray \(BA\):
\(\angle ABC\), \(\angle ABD\), \(\angle ABE\), \(\angle ABF\).
Each is the turn from \(BA\) to \(BC/BD/BE/BF\) that is \(<\;180^{\circ}\).
-
More angles at \(B\) starting from \(BC\):
\(\angle CBD\), \(\angle CBE\), \(\angle CBF\).
Again, take the smaller turn each time \(<\;180^{\circ}\).
-
Continue at \(B\) with next rays:
\(\angle DBE\), \(\angle DBF\), \(\angle EBF\).
All are clearly less than a straight angle \(180^{\circ}\).
-
Read rays at vertex \(A\):
Rays from \(A\): \(AB\), \(AC\), \(AD\), \(AE\), \(AF\).
Pick pairs that form minor angles in the figure:
\(\angle BAC\), \(\angle BAD\), \(\angle BAE\), \(\angle CAF\), \(\angle DAF\).
-
Check the count:
Total listed = \(4 + 3 + 3 + 5 = 15\) angles.
-
Final check:
None of the chosen pairs make a straight line, so each angle is \(<\;180^{\circ}\).
If any pair looked straight, we would skip it because a straight angle equals \(180^{\circ}\).
Note: Other correct sets of 15 minor angles are also possible if you pick different valid pairs.