NCERT Exemplar Solutions
Class 6 - Mathematics - Unit 2: Geometry - Problems and SolutionsQuestion 49
Class 6 - Mathematics - Unit 2: Geometry - Problems and Solutions
Question. 49
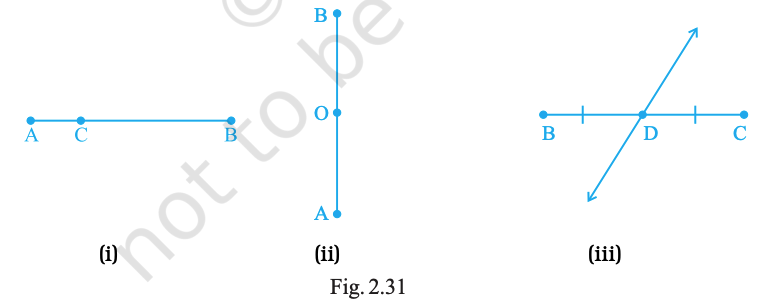
Which points in Fig. 2.31 appear to be mid-points of the line segments? When you locate a mid-point, name the two equal line segments formed by it.
Answer:
(i) C is the mid-point of \(\overline{AB}\); segments: AC and CB.
(ii) O is the mid-point of \(\overline{AB}\); segments: AO and OB.
(iii) D is the mid-point of \(\overline{BC}\); segments: BD and DC.
Detailed Answer with Explanation:
Key idea: A mid-point divides a line segment into two equal parts.
Write this as small steps:
- Take a segment, say \(\overline{AB}\).
- If a point \(M\) lies on \(\overline{AB}\) and makes the two parts equal, then
\(AM = MB\)
so \(M\) is the mid-point of \(\overline{AB}\).
(i) Point \(C\) on \(\overline{AB}\)
- From the figure, the two small segments look equal.
\(AC = CB\)
Therefore, \(C\) is the mid-point of \(\overline{AB}\).
The equal segments formed are:
\(\overline{AC}\) and \(\overline{CB}\).
(ii) Point \(O\) on \(\overline{AB}\)
- From the figure, the two parts on both sides of \(O\) appear equal.
\(AO = OB\)
Therefore, \(O\) is the mid-point of \(\overline{AB}\).
The equal segments formed are:
\(\overline{AO}\) and \(\overline{OB}\).
(iii) Point \(D\) on \(\overline{BC}\)
- From the figure, the two parts on both sides of \(D\) appear equal.
\(BD = DC\)
Therefore, \(D\) is the mid-point of \(\overline{BC}\).
The equal segments formed are:
\(\overline{BD}\) and \(\overline{DC}\).
Conclusion: In each case, the test is simple—check if the two smaller segments are equal. If yes, the point is a mid-point, and the names of the two equal segments are written accordingly.