NCERT Exemplar Solutions
Class 6 - Mathematics - Unit 2: Geometry - Problems and SolutionsQuestion 57
Class 6 - Mathematics - Unit 2: Geometry - Problems and Solutions
Question. 57
What is common in the following figures (i) and (ii) (Fig. 2.36)? Is Fig. 2.36(i) that of a triangle? If not, why?
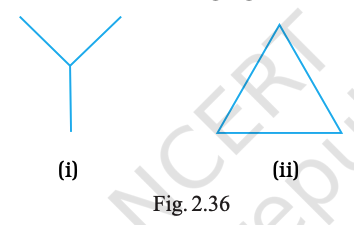
Answer:
Common feature: both are formed by three line segments.
Fig. 2.36(i) is not a triangle because the three segments do not form a closed figure (their ends are not joined).
Detailed Answer with Explanation:
Step 1: Look at both figures. Each is drawn using three straight line segments.
Step 2: Recall: A triangle is a closed shape made of three line segments. The ends (endpoints) must meet pairwise to make three corners.
Step 3: Check Fig. (i). The ends of the segments do not all meet. There is a gap. So the shape is open.
Step 4: An open shape cannot be a triangle. Therefore, Fig. (i) is not a triangle.
Step 5: Fig. (ii) has three segments whose ends meet and make a closed loop. That is a triangle.
Conclusion: Common: three line segments. Difference: only Fig. (ii) is a triangle because it is closed; Fig. (i) is open.