NCERT Exemplar Solutions
Class 6 - Mathematics - Unit 2: Geometry - Problems and SolutionsQuestion 44
Class 6 - Mathematics - Unit 2: Geometry - Problems and Solutions
Question. 44
State the mid-points of all the sides of Fig. 2.26.
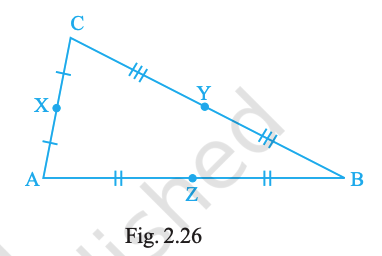
Answer:
Mid-point of \(AC\): X; mid-point of \(CB\): Y; mid-point of \(AB\): Z.
Detailed Answer with Explanation:
Idea: A mid-point divides a line segment into two equal parts.
-
Side \(AC\):
Tick marks at point \(X\) show the two parts are equal.
Write in small steps:
\(AX\) and \(XC\) are the two parts.
\(AX = XC\).
So, \(X\) is the mid-point of \(AC\).
-
Side \(CB\):
Tick marks at point \(Y\) show equality of the two parts.
\(CY\) and \(YB\) are the two parts.
\(CY = YB\).
So, \(Y\) is the mid-point of \(CB\).
-
Side \(AB\):
Tick marks at point \(Z\) show equality of the two parts.
\(AZ\) and \(ZB\) are the two parts.
\(AZ = ZB\).
So, \(Z\) is the mid-point of \(AB\).
Conclusion: Mid-points are \(X\) on \(AC\), \(Y\) on \(CB\), and \(Z\) on \(AB\).