NCERT Exemplar Solutions
Class 6 - Mathematics - Unit 2: Geometry - Problems and SolutionsQuestion 42
Class 6 - Mathematics - Unit 2: Geometry - Problems and Solutions
Question. 42
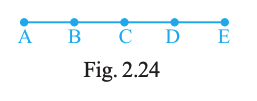
Name all the line segments in Fig. 2.24.
Answer:
AB, BC, CD, DE, AC, BD, CE, AD, BE, AE
Detailed Answer with Explanation:
Step 1: Understand what makes a line segment.
A line segment is formed by choosing any two points as its endpoints.
Step 2: Count how many points are given.
There are 5 points on the same line: A, B, C, D, E.
Step 3: Count how many different pairs of points we can choose.
We need the number of ways to choose 2 points out of 5.
Use combinations:
\(^5C_2\)
\(= \dfrac{5!}{2!\,3!}\)
\(= \dfrac{5\times4\times3\times2\times1}{(2\times1)(3\times2\times1)}\)
\(= \dfrac{20}{2}\)
\(= 10\)
Step 4: List all the 10 segments by pairing points.
AB, BC, CD, DE, AC, BD, CE, AD, BE, AE.
These are all the segments formed by every pair of the five points.