NCERT Exemplar Solutions
Class 6 - Mathematics - Unit 2: Geometry - Problems and SolutionsQuestion 59
Class 6 - Mathematics - Unit 2: Geometry - Problems and Solutions
Question. 59
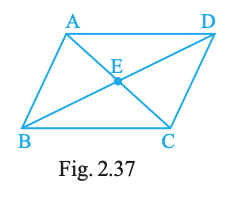
In Fig. 2.37, (a) name any four angles that appear to be acute angles. (b) name any two angles that appear to be obtuse angles.
Answer:
(a) Acute (any four): ∠AEB, ∠BEC, ∠CED, ∠DEA.
(b) Obtuse (any two): ∠ABC, ∠CDA.
Detailed Answer with Explanation:
Idea: First recall what "acute" and "obtuse" mean. Then read the picture.
Definitions:
Acute angle: measure is less than a right angle.
( ext{Acute: } m(angle) < 90^circ )
Obtuse angle: measure is more than a right angle but less than a straight angle.
( ext{Obtuse: } 90^circ < m(angle) < 180^circ )
Step 1: Look at point E
Two lines cross at ( E ) and make four small angles around ( E ).
Each of these looks smaller than a right angle.
So they are acute: ( angle AEB, angle BEC, angle CED, angle DEA ).
Step 2: Look at vertices B and D
Inside the quadrilateral, the angles at ( B ) and ( D ) open wider than a right angle.
So they are obtuse: ( angle ABC ) and ( angle CDA ).
Conclusion:
Any four acute around ( E ): ( angle AEB, angle BEC, angle CED, angle DEA ).
Any two obtuse at the corners: ( angle ABC, angle CDA ).