NCERT Exemplar Solutions
Class 6 - Mathematics - Unit 2: Geometry - Problems and SolutionsQuestion 51
Class 6 - Mathematics - Unit 2: Geometry - Problems and Solutions
Question. 51
Will the measure of ∠ABC and of ∠CBD make measure of ∠ABD in Fig. 2.32?
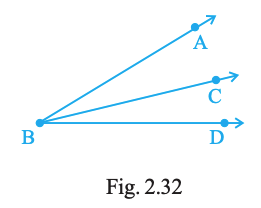
Answer:
Yes.
Detailed Answer with Explanation:
Think of the two angles placed next to each other at point B.
- Both angles have the same vertex: \(B\).
- They share a common arm: \(BC\).
- The other arms are different:
\(\angle ABC\): from \(BA\) to \(BC\)\(\angle CBD\): from \(BC\) to \(BD\)
- Such angles are called adjacent angles. When placed side by side, they form the bigger angle from \(BA\) to \(BD\): \(\angle ABD\).
- So their measures add up step by step:
\(\text{measure}(\angle ABC)\)\(+\ \text{measure}(\angle CBD)\)\(=\ \text{measure}(\angle ABD)\)
Therefore, adding \(\angle ABC\) and \(\angle CBD\) gives \(\angle ABD\).