NCERT Exemplar Solutions
Class 6 - Mathematics - Unit 2: Geometry - Problems and SolutionsQuestion 63
Class 6 - Mathematics - Unit 2: Geometry - Problems and Solutions
Question. 63
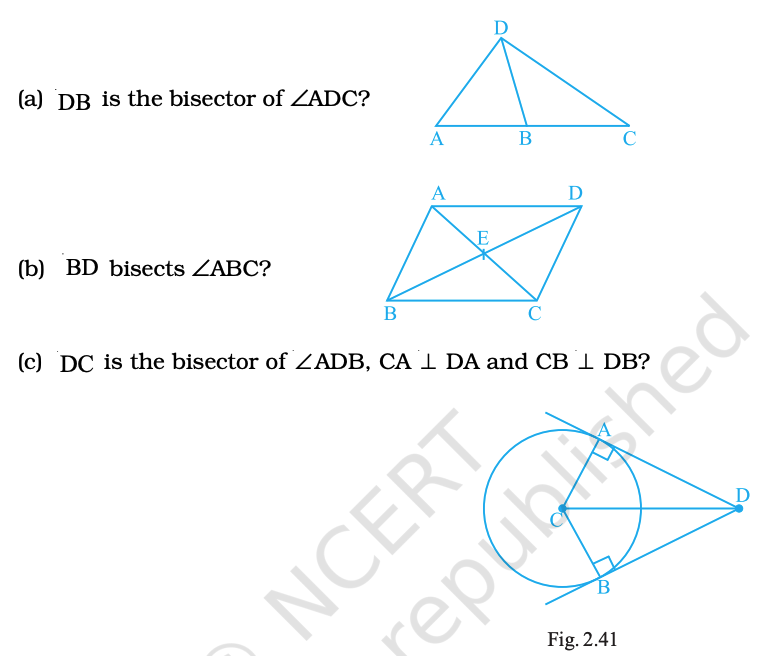
What conclusion can be drawn from each part of Fig. 2.41 if
(a) DB is the bisector of ∠ADC?
(b) BD bisects ∠ABC?
(c) DC is the bisector of ∠ADB, CA ⟂ DA and CB ⟂ DB?
Answer:
(a) ∠ADB = ∠BDC.
(b) ∠ABD = ∠DBC.
(c) DA and DB are tangents to the circle at A and B respectively; the tangents from D are equal, so DA = DB, and the line from the centre CD bisects the angle between them.
Detailed Answer with Explanation:
By definition of an angle bisector and the property “the line from the centre to an external point bisects the angle between the tangents; tangents from an external point are equal.”