NCERT Exemplar Solutions
Class 6 - Mathematics - Unit 2: Geometry - Problems and SolutionsQuestion 61
Class 6 - Mathematics - Unit 2: Geometry - Problems and Solutions
Question. 61
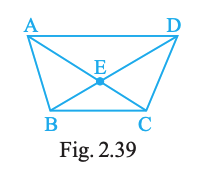
In Fig. 2.39, answer:
(a) What is AE + EC?
(b) What is AC − EC?
(c) What is BD − BE?
(d) What is BD − DE?
Answer:
(a) AC
(b) AE
(c) DE
(d) BE
Detailed Answer with Explanation:
E is the intersection of diagonals \(AC\) and \(BD\). Hence AE + EC = AC, AC − EC = AE, BD − BE = DE and BD − DE = BE.