NCERT Exemplar Solutions
Class 6 - Mathematics - Unit 2: Geometry - Multiple Choice QuestionsQuestion 15
Class 6 - Mathematics - Unit 2: Geometry - Multiple Choice Questions
Question. 15
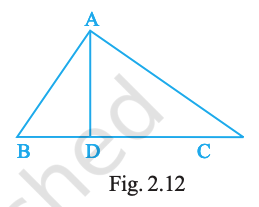
In Fig. 2.12, \(\angle BAC = 90°\) and AD ⟂ BC. The number of right triangles in the figure is
(A)
1
(B)
2
(C)
3
(D)
4
Detailed Answer with Explanation:
Step 1: A right triangle has one angle of \(90^\circ\).
Step 2: Given \(\angle BAC = 90^\circ\).
So, \(\triangle ABC\) is a right triangle.
Step 3: Also given AD ⟂ BC.
This means the angle at D with BC is a right angle.
Step 4: In \(\triangle ABD\):
\(\angle ADB = 90^\circ\).
So, \(\triangle ABD\) is a right triangle.
Step 5: In \(\triangle ADC\):
\(\angle ADC = 90^\circ\).
So, \(\triangle ADC\) is a right triangle.
Step 6: Count all right triangles.
\(\triangle ABC\) → 1
\(\triangle ABD\) → 1
\(\triangle ADC\) → 1
Total = \(1 + 1 + 1 = 3\).