NCERT Exemplar Solutions
Class 6 - Mathematics - Unit 2: Geometry - Multiple Choice QuestionsQuestion 8
Class 6 - Mathematics - Unit 2: Geometry - Multiple Choice Questions
Question. 8
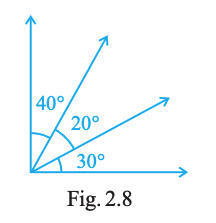
The number of angles in Fig. 2.8 is
(A)
3
(B)
4
(C)
5
(D)
6
Detailed Answer with Explanation:
Beginner-friendly steps
- In the figure, four rays meet at one point (the vertex). Name them in order as OA, OB, OC, OD.
- The small adjacent angles between these rays are given as:
\(\angle AOB = 40^{\circ}\)\(\angle BOC = 30^{\circ}\)\(\angle COD = 20^{\circ}\)
- Every pair of adjacent small angles makes a bigger angle. Add them:
\(\angle AOC = \angle AOB + \angle BOC = 40^{\circ} + 30^{\circ} = 70^{\circ}\)\(\angle BOD = \angle BOC + \angle COD = 30^{\circ} + 20^{\circ} = 50^{\circ}\)
- All three small angles together also make one angle:
\(\angle AOD = \angle AOB + \angle BOC + \angle COD = 40^{\circ} + 30^{\circ} + 20^{\circ} = 90^{\circ}\)
- Now count all distinct angles formed at the vertex:
Small: \(\angle AOB\), \(\angle BOC\), \(\angle COD\) → 3 anglesCombined: \(\angle AOC\), \(\angle BOD\), \(\angle AOD\) → 3 anglesTotal = \(3 + 3 = 6\)
Answer: Option D — 6 angles.