NCERT Solutions
Class 10 - Mathematics - Chapter 6: TRIANGLES - Exercise 6.2Question 1
Class 10 - Mathematics - Chapter 6: TRIANGLES - Exercise 6.2
Question. 1
In Fig. 6.17, (i) and (ii), DE \(\parallel\) BC. Find EC in (i) and AD in (ii).
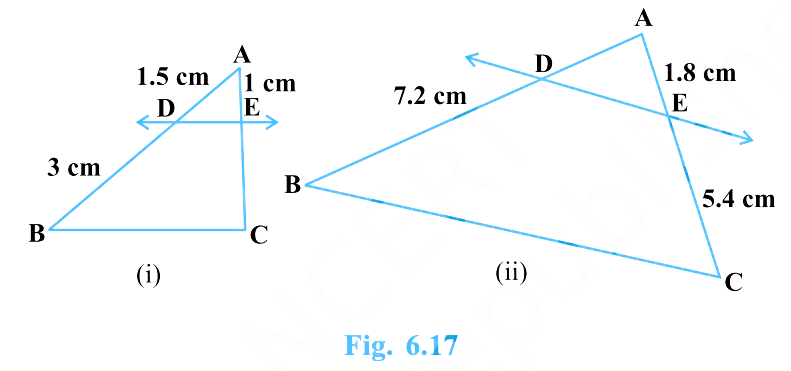
Answer:
(i) \(2\ \text{cm}\)
(ii) \(2.4\ \text{cm}\)
Detailed Answer with Explanation:
Since \(DE \parallel BC\), in both figures we have similar triangles \(\triangle ADE \sim \triangle ABC\). So,
\[\frac{AD}{AB} = \frac{AE}{AC} = \frac{DE}{BC}.\]
(i) Finding EC
On side \(AB\): \(BD = 3\,\text{cm}\) and \(AD = 1.5\,\text{cm}\). So
\[AB = AD + DB = 1.5 + 3 = 4.5\,\text{cm}.\]
On side \(AC\): \(AE = 1\,\text{cm}\) and \(EC\) is unknown, so
\[AC = AE + EC = 1 + EC.\]
Using similarity,
\[\frac{AD}{AB} = \frac{AE}{AC} \Rightarrow \frac{1.5}{4.5} = \frac{1}{1 + EC}.\]
Now, \(\dfrac{1.5}{4.5} = \dfrac{1}{3}\), so
\[\frac{1}{3} = \frac{1}{1 + EC} \Rightarrow 1 + EC = 3 \Rightarrow EC = 2\,\text{cm}.\]
(ii) Finding AD
On side \(AC\): \(AE = 1.8\,\text{cm}\) and \(EC = 5.4\,\text{cm}\). Hence
\[AC = AE + EC = 1.8 + 5.4 = 7.2\,\text{cm}.\]
On side \(AB\): \(BD = 7.2\,\text{cm}\) and \(AD\) is unknown, say \(AD = x\). Then
\[AB = AD + DB = x + 7.2.\]
Using similarity,
\[\frac{AD}{AB} = \frac{AE}{AC} \Rightarrow \frac{x}{x + 7.2} = \frac{1.8}{7.2}.\]
Simplify the right-hand side:
\[\frac{1.8}{7.2} = \frac{1}{4}.\]
So,
\[\frac{x}{x + 7.2} = \frac{1}{4} \Rightarrow 4x = x + 7.2 \Rightarrow 3x = 7.2 \Rightarrow x = 2.4.\]
Thus \(AD = 2.4\,\text{cm}.\)