NCERT Solutions
Class 10 - Mathematics - Chapter 6: TRIANGLES - Exercise 6.3Question 12
Class 10 - Mathematics - Chapter 6: TRIANGLES - Exercise 6.3
Question. 12
Sides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of \(\triangle PQR\) (see Fig. 6.41). Show that \(\triangle ABC \sim \triangle PQR\).
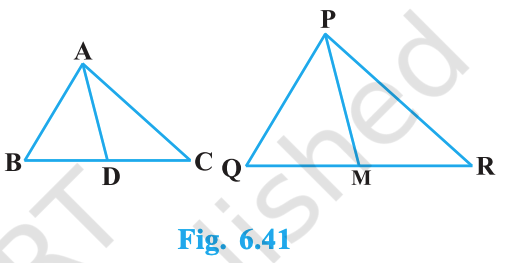
Detailed Answer with Explanation:
Given: In \(\triangle ABC\), AD is a median, so D is the midpoint of BC. In \(\triangle PQR\), PM is a median, so M is the midpoint of QR. Also, the three lengths are proportional:
\[\frac{AB}{PQ} = \frac{BC}{QR} = \frac{AD}{PM}.\tag{1}\]
To prove: \(\triangle ABC \sim \triangle PQR\).
Step 1: Express the smaller sides BD and QM
Since AD and PM are medians,
\[BD = DC = \frac{BC}{2}, \quad QM = MR = \frac{QR}{2}.\]
Using the second ratio in (1):
\[\frac{BC}{QR} = \frac{AB}{PQ}.\tag{2}\]
So,
\[\frac{BD}{QM} = \frac{\dfrac{BC}{2}}{\dfrac{QR}{2}} = \frac{BC}{QR} = \frac{AB}{PQ}.\tag{3}\]
Step 2: Prove \(\triangle ABD \sim \triangle PQM\) (SSS)
From (1) and (3), we have
\[\frac{AB}{PQ} = \frac{AD}{PM} = \frac{BD}{QM}.\]
Thus the three pairs of corresponding sides of \(\triangle ABD\) and \(\triangle PQM\) are proportional. Hence, by the SSS similarity criterion,
\[\triangle ABD \sim \triangle PQM.\]
This gives equality of corresponding angles:
\[\angle BAD = \angle QPM, \quad \angle ABD = \angle PQM.\tag{4}\]
Step 3: Transfer these angles to the big triangles
Since D lies on BC and M lies on QR, we have
\[\angle ABC = \angle ABD, \quad \angle PQR = \angle PQM,\]
and from (4),
\[\angle ABC = \angle ABD = \angle PQM = \angle PQR.\tag{5}\]
Similarly, at the vertices A and P,
\[\angle BAC = \angle BAD, \quad \angle QPR = \angle QPM,\]
so from (4),
\[\angle BAC = \angle BAD = \angle QPM = \angle QPR.\tag{6}\]
Step 4: Conclude similarity of \(\triangle ABC\) and \(\triangle PQR\)
From (5) and (6), we have two pairs of equal angles:
\[\angle ABC = \angle PQR, \quad \angle BAC = \angle QPR.\]
Therefore, by the AA similarity criterion,
\[\triangle ABC \sim \triangle PQR.\]
Hence proved.