NCERT Solutions
Class 10 - Mathematics - Chapter 6: TRIANGLES - Exercise 6.3Question 11
Class 10 - Mathematics - Chapter 6: TRIANGLES - Exercise 6.3
Question. 11
In Fig. 6.40, E is a point on side CB of an isosceles triangle ABC with \(AB = AC\). If AD ⟂ BC and EF ⟂ AC, prove that \(\triangle ABD \sim \triangle ECF\).
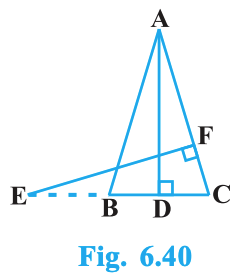
Detailed Answer with Explanation:
Given: \(\triangle ABC\) is isosceles with \(AB = AC\). E lies on side CB. AD is perpendicular to BC and EF is perpendicular to AC.
To prove: \(\triangle ABD \sim \triangle ECF\).
Step 1: Mark the right angles
Since AD ⟂ BC, angle at D in \(\triangle ABD\) is a right angle:
\[\angle ADB = 90^\circ.\]
Since EF ⟂ AC, angle at F in \(\triangle ECF\) is a right angle:
\[\angle EFC = 90^\circ.\]
Thus,
\[\angle ADB = \angle EFC. \tag{1}\]
Step 2: Use the isosceles property \(AB = AC\)
In an isosceles triangle ABC with \(AB = AC\), the base angles at B and C are equal:
\[\angle ABC = \angle BCA. \tag{2}\]
Step 3: Relate angles in the two smaller triangles
In \(\triangle ABD\), angle at B is
\[\angle ABD = \angle ABC,\]
because BD lies along BC.
In \(\triangle ECF\), angle at C is
\[\angle ECF = \angle BCA,\]
because CE lies along CB and CF lies along CA.
Using (2):
\[\angle ABD = \angle ABC = \angle BCA = \angle ECF. \tag{3}\]
Step 4: Conclude similarity
From (1) and (3), we have two pairs of equal angles:
\[\angle ADB = \angle EFC, \quad \angle ABD = \angle ECF.\]
Therefore, by the AA similarity criterion,
\[\triangle ABD \sim \triangle ECF.\]
Hence proved.