NCERT Solutions
Class 10 - Mathematics - Chapter 6: TRIANGLES - Exercise 6.3Question 2
Class 10 - Mathematics - Chapter 6: TRIANGLES - Exercise 6.3
Question. 2
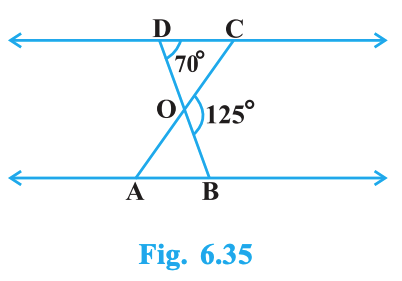
In Fig. 6.35, \(\triangle ODC \sim \triangle OBA\), \(\angle BOC = 125^\circ\) and \(\angle CDO = 70^\circ\). Find \(\angle DOC\), \(\angle DCO\) and \(\angle OAB\).
Answer:
\(55^\circ,\ 55^\circ,\ 55^\circ\)
Detailed Answer with Explanation:
Step 1: Find \(\angle DOC\).
Points \(B, O, D\) are collinear and points \(C, O, A\) are collinear. So \(\angle BOC\) and \(\angle COD\) form a linear pair.
\[\angle BOC + \angle COD = 180^\circ\]
Given \(\angle BOC = 125^\circ\):
\[125^\circ + \angle COD = 180^\circ \Rightarrow \angle COD = 55^\circ\]
So,
\[\angle DOC = 55^\circ.\]
Step 2: Find \(\angle DCO\).
In \(\triangle ODC\):
\[\angle CDO + \angle DOC + \angle DCO = 180^\circ\]
Given \(\angle CDO = 70^\circ\) and \(\angle DOC = 55^\circ\):
\[70^\circ + 55^\circ + \angle DCO = 180^\circ\]
\[125^\circ + \angle DCO = 180^\circ \Rightarrow \angle DCO = 55^\circ\]
Step 3: Find \(\angle OAB\).
The lines through \(D\) and \(C\) are parallel to the lines through \(A\) and \(B\) (top and bottom horizontal lines are parallel). Also, \(A, O, C\) are collinear and \(B\) lies on the line parallel to \(DC\).
Thus, angle \(\angle OAB\) (between \(AO\) and \(AB\)) equals angle between \(CO\) and \(CD\):
\[\angle OAB = \angle OCD = \angle DCO = 55^\circ\]
Conclusion:
\[\angle DOC = 55^\circ, \quad \angle DCO = 55^\circ, \quad \angle OAB = 55^\circ.\]