NCERT Solutions
Class 10 - Mathematics - Chapter 6: TRIANGLES - Exercise 6.3Question 1
Class 10 - Mathematics - Chapter 6: TRIANGLES - Exercise 6.3
Question. 1
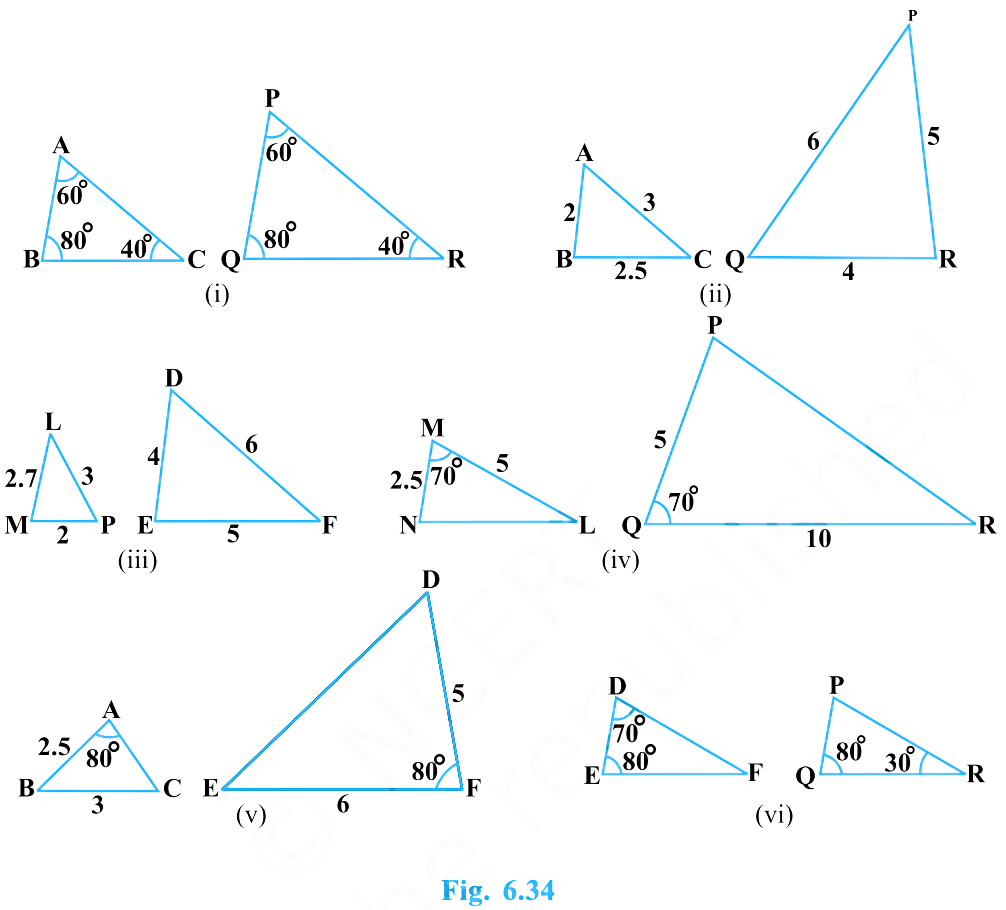
State which pairs of triangles in Fig. 6.34 are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in symbolic form:
(i)
(ii)
(iii)
(iv)
(v)
(vi)
Answer:
(i) Yes. AAA, \(\triangle ABC \sim \triangle PQR\)
(ii) Yes. SSS, \(\triangle ABC \sim \triangle QRP\)
(iii) No
(iv) Yes. SAS, \(\triangle MNL \sim \triangle QPR\)
(v) No
(vi) Yes. AA, \(\triangle DEF \sim \triangle PQR\)
Detailed Answer with Explanation:
(i)
In \(\triangle ABC\), the angles are \(60^\circ, 80^\circ, 40^\circ\). In \(\triangle PQR\), the angles are also \(60^\circ, 80^\circ, 40^\circ\). Since all three corresponding angles are equal,
\(\triangle ABC \sim \triangle PQR \quad (\text{AAA similarity}).\)
(ii)
In \(\triangle ABC\), the sides are \(AB = 2,\ BC = 2.5,\ AC = 3\).
In \(\triangle QRP\), the sides are \(QR = 4,\ RP = 5,\ QP = 6\).
The ratios of corresponding sides are
\[\frac{AB}{QR} = \frac{2}{4} = \frac{1}{2},\quad \frac{BC}{RP} = \frac{2.5}{5} = \frac{1}{2},\quad \frac{AC}{QP} = \frac{3}{6} = \frac{1}{2}.\]
All three ratios are equal, so
\[\triangle ABC \sim \triangle QRP \quad (\text{SSS similarity}).\]
(iii)
\(\triangle LMP\) has sides \(LM = 2.7,\ MP = 2,\ LP = 3\).
\(\triangle DEF\) has sides \(DE = 4,\ EF = 5,\ DF = 6\).
The side ratios are not all equal (e.g. \(2.7/4 \neq 2/5\)), so no constant scale factor exists for all three sides. Thus the triangles are not similar.
(iv)
In \(\triangle MNL\), sides around angle \(M\) are \(MN = 2.5\) and \(ML = 5\), with included angle \(\angle M = 70^\circ\).
In \(\triangle QPR\), sides around angle \(Q\) are \(QP = 5\) and \(QR = 10\), with included angle \(\angle Q = 70^\circ\).
The side ratios are
\[\frac{MN}{QP} = \frac{2.5}{5} = \frac{1}{2},\quad \frac{ML}{QR} = \frac{5}{10} = \frac{1}{2},\]
and the included angles are equal: \(\angle M = \angle Q = 70^\circ\). So
\[\triangle MNL \sim \triangle QPR \quad (\text{SAS similarity}).\]
(v)
In the first triangle, two sides and the included angle are \(AB = 2.5,\ BC = 3,\ \angle A = 80^\circ\).
In the second triangle, two sides and included angle are \(EF = 6,\ FD = 5,\ \angle F = 80^\circ\).
The ratios of the corresponding sides around the equal angle are
\[\frac{AB}{EF} = \frac{2.5}{6},\quad \frac{BC}{FD} = \frac{3}{5},\]
which are not equal, so the SAS condition is not satisfied. The three side ratios are also not all equal, so SSS fails too. Hence the triangles are not similar.
(vi)
In \(\triangle DEF\), two angles are \(\angle D = 70^\circ\) and \(\angle E = 80^\circ\).
In \(\triangle PQR\), two angles are \(\angle Q = 70^\circ\) and \(\angle P = 80^\circ\).
So,
\[\angle D = \angle Q,\quad \angle E = \angle P.\]
Two pairs of corresponding angles are equal, therefore
\[\triangle DEF \sim \triangle PQR \quad (\text{AA/AAA similarity}).\]