NCERT Solutions
Class 10 - Mathematics - Chapter 6: TRIANGLES - Exercise 6.3Question 4
Class 10 - Mathematics - Chapter 6: TRIANGLES - Exercise 6.3
Question. 4
In Fig. 6.36, \(\dfrac{QR}{QS} = \dfrac{QT}{PR}\) and \(\angle 1 = \angle 2\). Show that \(\triangle PQS \sim \triangle TQR\).
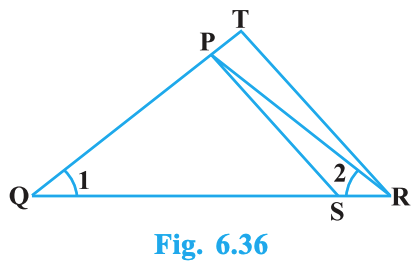
Detailed Answer with Explanation:
Given: In Fig. 6.36,
- \(\dfrac{QR}{QS} = \dfrac{QT}{PR}\)
- \(\angle 1 = \angle 2\)
To prove: \(\triangle PQS \sim \triangle TQR\).
Step 1: Use the angle condition in \(\triangle PQR\)
Angles \(\angle 1\) and \(\angle 2\) are the base angles of \(\triangle PQR\):
\[\angle 1 = \angle PQR, \quad \angle 2 = \angle PRQ\]
Given \(\angle 1 = \angle 2\), so
\[\angle PQR = \angle PRQ.\]
In a triangle, sides opposite equal angles are equal, therefore
\[PQ = PR. \tag{1}\]
Step 2: Rewrite the given side ratio using (1)
Given:
\[\frac{QR}{QS} = \frac{QT}{PR}.\]
Using \(PR = PQ\) from (1):
\[\frac{QR}{QS} = \frac{QT}{PQ}. \tag{2}\]
Step 3: Compare sides around the common angle at \(Q\)
Consider \(\triangle PQS\) and \(\triangle TQR\).
- In \(\triangle PQS\), the sides including \(\angle Q\) are \(QP\) and \(QS\).
- In \(\triangle TQR\), the sides including \(\angle Q\) are \(QT\) and \(QR\).
From (2):
\[\frac{QR}{QS} = \frac{QT}{QP} \quad \Longrightarrow \quad \frac{QS}{QR} = \frac{QP}{QT}. \tag{3}\]
Also, \(\angle PQS\) and \(\angle TQR\) are the same angle at \(Q\):
\[\angle PQS = \angle TQR = \angle Q. \tag{4}\]
Step 4: Apply SAS similarity criterion
From (3), the pairs of corresponding sides around angle \(Q\) are proportional:
\[\frac{QS}{QR} = \frac{QP}{QT}.\]
From (4), the included angle between these sides in both triangles is equal.
Therefore, by the SAS similarity criterion,
\[\triangle PQS \sim \triangle TQR.\]
Hence proved.