NCERT Solutions
Class 10 - Mathematics - Chapter 6: TRIANGLES - Exercise 6.3Question 7
Class 10 - Mathematics - Chapter 6: TRIANGLES - Exercise 6.3
Question. 7
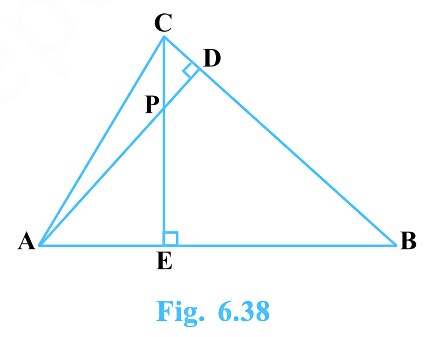
In Fig. 6.38, altitudes AD and CE of \(\triangle ABC\) intersect at P. Show that:
(i) \(\triangle AEP \sim \triangle CDP\)
(ii) \(\triangle ABD \sim \triangle CBE\)
(iii) \(\triangle AEP \sim \triangle ADB\)
(iv) \(\triangle PDC \sim \triangle BEC\)
Detailed Answer with Explanation:
Given: In \(\triangle ABC\), AD and CE are altitudes, so
\[AD \perp BC, \quad CE \perp AB.\]
They intersect at P.
To prove: The four pairs of triangles are similar as stated.
(i) Prove \(\triangle AEP \sim \triangle CDP\)
Since CE is an altitude, \(CE \perp AB\). Thus
\[\angle AEP = 90^\circ.\]
Since AD is an altitude, \(AD \perp BC\). As D lies on BC and P lies on AD,
\[\angle CDP = 90^\circ.\]
Also, AP and PD lie on the same line AD, and EP and CP lie on the same line CE, so angle between AP and EP equals angle between CP and PD:
\[\angle APE = \angle CPD.\]
Therefore, we have two pairs of equal angles:
\[\angle AEP = \angle CDP = 90^\circ, \quad \angle APE = \angle CPD.\]
Hence, by AA similarity,
\[\triangle AEP \sim \triangle CDP.\]
(ii) Prove \(\triangle ABD \sim \triangle CBE\)
From the altitudes:
\[\angle ADB = 90^\circ, \quad \angle CEB = 90^\circ.\]
Point D lies on BC, so BD is a part of BC; point E lies on AB, so BE is a part of AB. Therefore the angle at B in both triangles is the same angle \(\angle ABC\):
\[\angle ABD = \angle CBE = \angle ABC.\]
Thus,
\[\angle ADB = \angle CEB, \quad \angle ABD = \angle CBE.\]
By AA similarity,
\[\triangle ABD \sim \triangle CBE.\]
(iii) Prove \(\triangle AEP \sim \triangle ADB\)
Again, \(CE \perp AB\) and \(AD \perp BC\). So
\[\angle AEP = 90^\circ, \quad \angle ADB = 90^\circ.\]
Now compare angles at A:
In \(\triangle AEP\), \(\angle PAE\) is the angle between AP (along AD) and AE (along AB).
In \(\triangle ADB\), \(\angle DAB\) is the angle between AD and AB.
Since AP lies on AD and AE lies on AB,
\[\angle PAE = \angle DAB.\]
Thus, two angles are equal:
\[\angle AEP = \angle ADB, \quad \angle PAE = \angle DAB.\]
Hence, by AA similarity,
\[\triangle AEP \sim \triangle ADB.\]
(iv) Prove \(\triangle PDC \sim \triangle BEC\)
From the altitudes, as before:
\[\angle PDC = 90^\circ \quad (AD \perp BC),\]
\[\angle BEC = 90^\circ \quad (CE \perp AB).\]
Now consider angles at C:
In \(\triangle PDC\), \(\angle PCD\) is the angle between CP (along CE) and CD (along CB).
In \(\triangle BEC\), \(\angle ECB\) is the angle between EC and CB.
So,
\[\angle PCD = \angle ECB.\]
Therefore,
\[\angle PDC = \angle BEC, \quad \angle PCD = \angle ECB.\]
By AA similarity,
\[\triangle PDC \sim \triangle BEC.\]
Thus, all four required pairs of triangles are similar.