NCERT Solutions
Class 10 - Mathematics - Chapter 6: TRIANGLES - Exercise 6.3Question 9
Class 10 - Mathematics - Chapter 6: TRIANGLES - Exercise 6.3
Question. 9
In Fig. 6.39, ABC and AMP are two right triangles right-angled at B and M respectively. Prove that:
(i) \(\triangle ABC \sim \triangle AMP\)
(ii) \(\dfrac{CA}{PA} = \dfrac{BC}{MP}\)
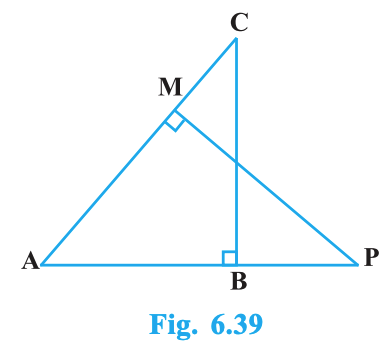
Detailed Answer with Explanation:
Given: \(\triangle ABC\) and \(\triangle AMP\) are right-angled at B and M respectively.
To prove: (i) \(\triangle ABC \sim \triangle AMP\); (ii) \(\dfrac{CA}{PA} = \dfrac{BC}{MP}\).
(i) Prove \(\triangle ABC \sim \triangle AMP\)
In \(\triangle ABC\),
\[\angle ABC = 90^\circ.\]
In \(\triangle AMP\),
\[\angle AMR = 90^\circ, \text{ i.e. } \angle AM P = 90^\circ.\]
So one angle of each triangle is a right angle.
Also, both triangles share angle at A:
\[\angle BAC = \angle PAM \quad (\text{common angle at } A).\]
Thus we have two pairs of equal angles:
\[\angle ABC = \angle AMP = 90^\circ, \quad \angle BAC = \angle PAM.\]
Therefore, by AA similarity,
\[\triangle ABC \sim \triangle AMP.\]
(ii) Prove \(\dfrac{CA}{PA} = \dfrac{BC}{MP}\)
From the similarity \(\triangle ABC \sim \triangle AMP\), corresponding vertices are:
\[A \leftrightarrow A, \quad B \leftrightarrow M, \quad C \leftrightarrow P.\]
So the corresponding sides are:
- \(AC \leftrightarrow AP\) (hypotenuses)
- \(BC \leftrightarrow MP\) (sides opposite the equal acute angles at A)
Hence, the ratio of corresponding sides is equal:
\[\frac{CA}{PA} = \frac{BC}{MP}.\]
Thus: (i) \(\triangle ABC \sim \triangle AMP\) and (ii) \(\dfrac{CA}{PA} = \dfrac{BC}{MP}\) are proved.