NCERT Solutions
Class 10 - Mathematics - Chapter 7: COORDINATE GEOMETRYExercise 7.2
Class 10 - Mathematics - Chapter 7: COORDINATE GEOMETRY
Question. 1
Find the coordinates of the point which divides the join of (−1, 7) and (4, −3) in the ratio 2 : 3.
Answer:
(1, 3)
Question. 2
Find the coordinates of the points of trisection of the line segment joining (4, −1) and (−2, −3).
Answer:
\(\left(2, -\dfrac{5}{3}\right)\) and \(\left(0, -\dfrac{7}{3}\right)\)
Question. 3
To conduct Sports Day activities, in your rectangular shaped school ground ABCD, lines have been drawn with chalk powder at a distance of 1 m each. 100 flower pots have been placed at a distance of 1 m from each other along AD, as shown in Fig. 7.12. Niharika runs \(\tfrac{1}{4}\)th the distance AD on the 2nd line and posts a green flag. Preet runs \(\tfrac{1}{5}\)th the distance AD on the eighth line and posts a red flag. What is the distance between both the flags? If Rashmi has to post a blue flag exactly halfway between the line segment joining the two flags, where should she post her flag?
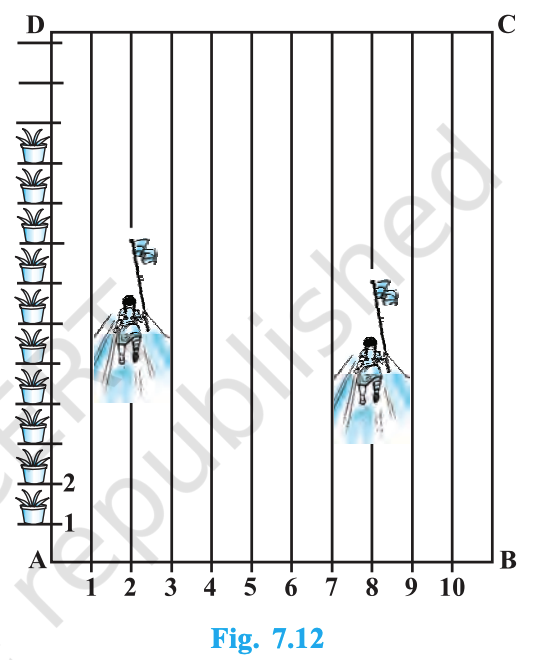
Answer:
Distance between the flags = \(\sqrt{61}\) m.
Rashmi should post the blue flag on the 5th line at a distance of 22.5 m.
Question. 4
Find the ratio in which the line segment joining the points (−3, 10) and (6, −8) is divided by (−1, 6).
Answer:
2 : 7
Question. 5
Find the ratio in which the line segment joining A(1, −5) and B(−4, 5) is divided by the x-axis. Also find the coordinates of the point of division.
Answer:
Ratio = 1 : 1
Point of division = \(\left(-\dfrac{3}{2}, 0\right)\)
Question. 6
If (1, 2), (4, y), (x, 6) and (3, 5) are the vertices of a parallelogram taken in order, find x and y.
Answer:
\(x = 6,\ y = 3\)
Question. 7
Find the coordinates of a point A, where AB is the diameter of a circle whose centre is (2, −3) and B is (1, 4).
Answer:
A = (3, −10)
Question. 8
If A and B are (−2, −2) and (2, −4), respectively, find the coordinates of P such that \(AP = \dfrac{3}{7} AB\) and P lies on the line segment AB.
Answer:
P = \(\left(-\dfrac{2}{7}, -\dfrac{20}{7}\right)\)
Question. 9
Find the coordinates of the points which divide the line segment joining A(−2, 2) and B(2, 8) into four equal parts.
Answer:
\(\left(-1, \dfrac{7}{2}\right), (0, 5), \left(1, \dfrac{13}{2}\right)\)
Question. 10
Find the area of a rhombus if its vertices are (3, 0), (4, 5), (−1, 4) and (−2, −1) taken in order. (Hint: Area of a rhombus \(= \dfrac{1}{2}\) × product of its diagonals.)
Answer:
24 sq. units