NCERT Solutions
Class 10 - Mathematics - Chapter 6: TRIANGLES - Exercise 6.2Question 3
Class 10 - Mathematics - Chapter 6: TRIANGLES - Exercise 6.2
Question. 3
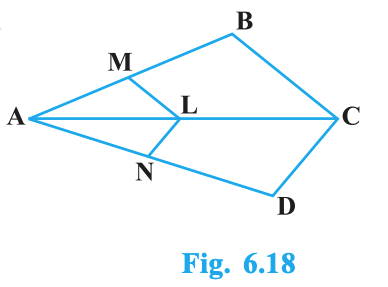
In Fig. 6.18, if LM \(\parallel\) CB and LN \(\parallel\) CD, prove that
\[\dfrac{AM}{AB} = \dfrac{AN}{AD}.\]
Answer:
\(\dfrac{AM}{AB} = \dfrac{AN}{AD}\)
Detailed Answer with Explanation:
Given: In Fig. 6.18, LM \(\parallel\) CB and LN \(\parallel\) CD.
1. Use LM \(\parallel\) CB
Consider \(\triangle ABC\) with points \(M\) on \(AB\) and \(L\) on \(AC\), and \(LM \parallel CB\).
Then,
\(\angle AML = \angle ABC\) (corresponding angles)
\(\angle ALM = \angle ACB\) (corresponding angles)
So, \(\triangle AML \sim \triangle ABC\) (AA similarity).
From similarity, corresponding sides are proportional:
\[\frac{AM}{AB} = \frac{AL}{AC} \quad ...(1)\]
2. Use LN \(\parallel\) CD
Now consider \(\triangle ADC\) with points \(N\) on \(AD\) and \(L\) on \(AC\), and \(LN \parallel CD\).
Then,
\(\angle ANL = \angle ADC\) (corresponding angles)
\(\angle ALN = \angle ACD\) (corresponding angles)
So, \(\triangle ALN \sim \triangle ADC\) (AA similarity).
Again, corresponding sides are proportional:
\[\frac{AN}{AD} = \frac{AL}{AC} \quad ...(2)\]
3. Compare the two ratios
From (1): \(\dfrac{AM}{AB} = \dfrac{AL}{AC}\)
From (2): \(\dfrac{AN}{AD} = \dfrac{AL}{AC}\)
Since both are equal to \(\dfrac{AL}{AC}\), we get
\[\frac{AM}{AB} = \frac{AN}{AD}.\]
Hence proved.