NCERT Solutions
Class 10 - Mathematics - Chapter 6: TRIANGLES - Exercise 6.2Question 4
Class 10 - Mathematics - Chapter 6: TRIANGLES - Exercise 6.2
Question. 4
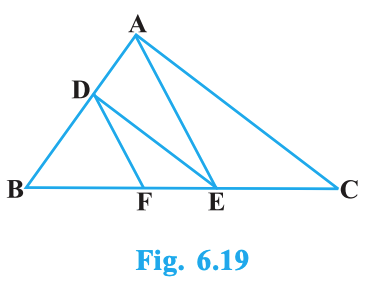
In Fig. 6.19, DE \(\parallel\) AC and DF \(\parallel\) AE. Prove that
\[\dfrac{BF}{FE} = \dfrac{BE}{EC}.\]
Answer:
\(\dfrac{BF}{FE} = \dfrac{BE}{EC}\)
Detailed Answer with Explanation:
Given: In \(\triangle ABC\), points \(D\) lies on \(AB\), and \(E, F\) lie on \(BC\). Lines are drawn so that \(DE \parallel AC\) and \(DF \parallel AE\).
To prove: \(\dfrac{BF}{FE} = \dfrac{BE}{EC}\).
Step 1: Use similarity in \(\triangle ABC\)
Since \(DE \parallel AC\) and \(D\) is on \(AB\), \(E\) is on \(BC\), we have:
\[\triangle BDE \sim \triangle BAC \quad (\text{AA similarity})\]
So the corresponding sides are proportional:
\[\frac{BD}{BA} = \frac{BE}{BC} = \frac{DE}{AC} \quad \text{...(1)}\]
Step 2: Use similarity in \(\triangle ABE\)
Since \(DF \parallel AE\) and \(D\) is on \(AB\), \(F\) is on \(BE\), we have:
\[\triangle BDF \sim \triangle BAE \quad (\text{AA similarity})\]
Thus,
\[\frac{BD}{BA} = \frac{BF}{BE} = \frac{DF}{AE} \quad \text{...(2)}\]
Step 3: Relate \(BF\) and \(BE\) using (1) and (2)
From (1) and (2), the common ratio is \(\dfrac{BD}{BA}\). Hence,
\[\frac{BE}{BC} = \frac{BD}{BA} = \frac{BF}{BE}\]
So,
\[\frac{BF}{BE} = \frac{BE}{BC} \quad \text{...(3)}\]
Step 4: Express segments on \(BC\)
Points \(B, F, E, C\) lie on the same straight line in that order, so:
\[BC = BE + EC, \quad BE = BF + FE\]
From (3):
\[BF \cdot BC = BE^2\]
Substitute \(BC = BE + EC\):
\[BF(BE + EC) = BE^2\]
\[BF \cdot BE + BF \cdot EC = BE^2\]
But \(BE = BF + FE\), so:
\[BE^2 = BE(BF + FE) = BF \cdot BE + BE \cdot FE\]
Comparing with the previous expression:
\[BF \cdot BE + BF \cdot EC = BF \cdot BE + BE \cdot FE\]
Cancel \(BF \cdot BE\) from both sides:
\[BF \cdot EC = BE \cdot FE\]
Step 5: Form the required ratio
Divide both sides by \(FE \cdot EC\) (non-zero):
\[\frac{BF}{FE} = \frac{BE}{EC}\]
Hence proved.