NCERT Solutions
Class 10 - Mathematics - Chapter 6: TRIANGLES - Exercise 6.2Question 5
Class 10 - Mathematics - Chapter 6: TRIANGLES - Exercise 6.2
Question. 5
In Fig. 6.20, DE \(\parallel\) OQ and DF \(\parallel\) OR. Show that \(EF \parallel QR\).
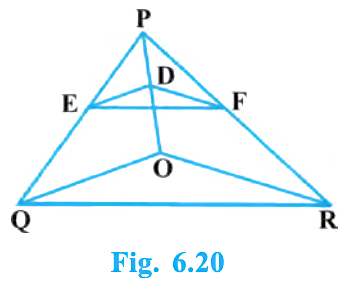
Answer:
\(EF \parallel QR\)
Detailed Answer with Explanation:
Given: In \(\triangle PQR\), point \(O\) lies on \(QR\). On segments \(PQ\) and \(PR\), points \(E\) and \(F\) are taken, and on \(PO\) point \(D\) is taken such that
\(DE \parallel OQ\) and \(DF \parallel OR\).
To prove: \(EF \parallel QR\).
Step 1: Use DE \(\parallel\) OQ in \(\triangle POQ\)
In \(\triangle POQ\), we have \(D\) on \(PO\), \(E\) on \(PQ\) and \(DE \parallel OQ\).
So, \(\triangle PDE \sim \triangle POQ\) (AA similarity).
Thus, corresponding sides are proportional:
\[\frac{PE}{PQ} = \frac{PD}{PO} \quad ...(1)\]
Step 2: Use DF \(\parallel\) OR in \(\triangle POR\)
In \(\triangle POR\), we have \(D\) on \(PO\), \(F\) on \(PR\) and \(DF \parallel OR\).
So, \(\triangle PDF \sim \triangle POR\) (AA similarity).
Hence,
\[\frac{PF}{PR} = \frac{PD}{PO} \quad ...(2)\]
Step 3: Compare the ratios
From (1) and (2):
\[\frac{PE}{PQ} = \frac{PD}{PO} = \frac{PF}{PR}\]
Thus,
\[\frac{PE}{PQ} = \frac{PF}{PR} \quad ...(3)\]
Step 4: Apply Converse of Basic Proportionality Theorem
In \(\triangle PQR\), points \(E\) and \(F\) lie on \(PQ\) and \(PR\) respectively, and we have shown that
\[\frac{PE}{PQ} = \frac{PF}{PR}.\]
By the Converse of Basic Proportionality Theorem, if a line through two sides of a triangle divides them in the same ratio, that line is parallel to the third side.
Therefore, line \(EF\) is parallel to \(QR\).
Hence proved that \(EF \parallel QR\).