NCERT Solutions
Class 10 - Mathematics - Chapter 7: COORDINATE GEOMETRY - Exercise 7.1Question 5
Class 10 - Mathematics - Chapter 7: COORDINATE GEOMETRY - Exercise 7.1
Question. 5
In a classroom, 4 friends are seated at the points A, B, C and D as shown in Fig. 7.8. Champa and Chameli walk into the class and after observing for a few minutes Champa asks Chameli, “Don’t you think ABCD is a square?” Chameli disagrees. Using the distance formula, find which of them is correct.
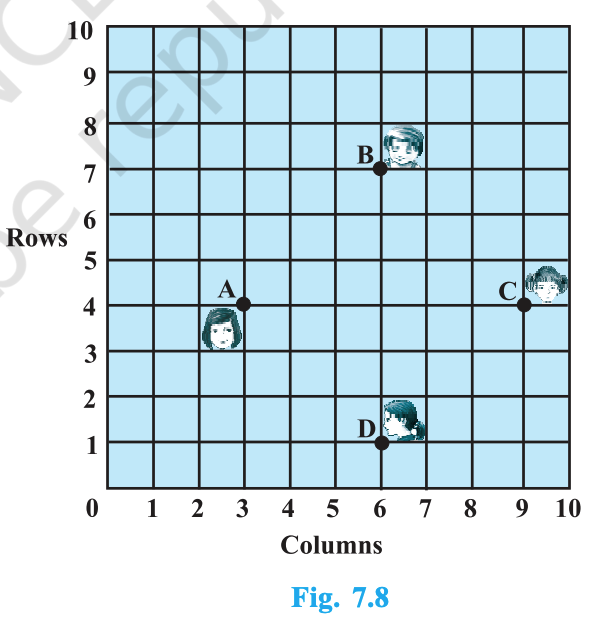
Answer:
Champa is correct.
Detailed Answer with Explanation:
From the grid we read the coordinates of the four friends as \(A(3, 4)\), \(B(6, 7)\), \(C(9, 4)\) and \(D(6, 1)\).
To decide whether \(ABCD\) is a square, we first find the lengths of all four sides using the distance formula between two points \((x_1, y_1)\) and \((x_2, y_2)\): \( d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \).
Side \(AB\): \( AB = \sqrt{(6 - 3)^2 + (7 - 4)^2} = \sqrt{3^2 + 3^2} = \sqrt{9 + 9} = \sqrt{18} = 3\sqrt{2} \).
Side \(BC\): \( BC = \sqrt{(9 - 6)^2 + (4 - 7)^2} = \sqrt{3^2 + (-3)^2} = \sqrt{9 + 9} = \sqrt{18} = 3\sqrt{2} \).
Side \(CD\): \( CD = \sqrt{(6 - 9)^2 + (1 - 4)^2} = \sqrt{(-3)^2 + (-3)^2} = \sqrt{9 + 9} = \sqrt{18} = 3\sqrt{2} \).
Side \(DA\): \( DA = \sqrt{(3 - 6)^2 + (4 - 1)^2} = \sqrt{(-3)^2 + 3^2} = \sqrt{9 + 9} = \sqrt{18} = 3\sqrt{2} \).
Thus all four sides are equal in length, each being \(3\sqrt{2}\).
Next, we check the diagonals.
Diagonal \(AC\): \( AC = \sqrt{(9 - 3)^2 + (4 - 4)^2} = \sqrt{6^2 + 0^2} = \sqrt{36} = 6 \).
Diagonal \(BD\): \( BD = \sqrt{(6 - 6)^2 + (1 - 7)^2} = \sqrt{0^2 + (-6)^2} = \sqrt{36} = 6 \).
Both diagonals are equal, and all four sides are equal, so \(ABCD\) is a square. Therefore, Champa is correct.