NCERT Exemplar Solutions
Class 10 - Mathematics - CHAPTER 11: Area Related To CirclesExercise 11.2
Class 10 - Mathematics - CHAPTER 11: Area Related To Circles
Question. 1
Is the area of the circle inscribed in a square of side a cm equal to \(\pi a^2\) cm²?
Answer:
Open
Question. 2
Will it be true to say that the perimeter of a square circumscribing a circle of radius a cm is \(8a\) cm?
Answer:
Open
Question. 3
In Fig. 11.3, a square is inscribed in a circle of diameter \(d\) and another square circumscribes the circle. Is the area of the outer square four times the area of the inner square?
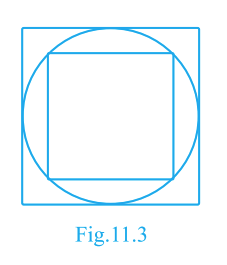
Answer:
Open
Question. 4
Is it true that the area of a segment of a circle is less than the area of its corresponding sector? Why?
Answer:
Open
Question. 5
Is it true that the distance travelled by a circular wheel of diameter \(d\) cm in one revolution is \(2\pi d\) cm? Why?
Answer:
Open
Question. 6
In covering a distance \(s\) metres, a circular wheel of radius \(r\) metres makes \(\dfrac{s}{2\pi r}\) revolutions. Is this statement true? Why?
Answer:
Open
Question. 7
The numerical value of the area of a circle is greater than the numerical value of its circumference. Is this statement true? Why?
Answer:
Open
Question. 8
If the length of an arc of a circle of radius \(r\) equals that of an arc of a circle of radius \(2r\), then the angle of the sector of the first circle is double the angle of the sector of the second circle. Is this statement false? Why?
Answer:
Open
Question. 9
The areas of two sectors of two different circles with equal corresponding arc lengths are equal. Is this statement true? Why?
Answer:
Open
Question. 10
The areas of two sectors of two different circles are equal. Is it necessary that their corresponding arc lengths are equal? Why?
Answer:
Open
Question. 11
Is the area of the largest circle that can be drawn inside a rectangle of length \(a\) cm and breadth \(b\) cm (\(a>b\)) equal to \(\pi b^2\) cm²? Why?
Answer:
Open
Question. 12
Circumferences of two circles are equal. Is it necessary that their areas are equal? Why?
Answer:
Open
Question. 13
Areas of two circles are equal. Is it necessary that their circumferences are equal? Why?
Answer:
Open
Question. 14
Is it true to say that the area of a square inscribed in a circle of diameter \(p\) cm is \(p^2\) cm²? Why?