NCERT Exemplar Solutions
Class 10 - Mathematics - CHAPTER 11: Area Related To CirclesExercise 11.3
Class 10 - Mathematics - CHAPTER 11: Area Related To Circles
Question. 1
Find the radius of a circle whose circumference is equal to the sum of the circumferences of two circles of radii 15 cm and 18 cm.
Answer:
33 cm
Open
Question. 2
In Fig. 11.5, a square of diagonal 8 cm is inscribed in a circle. Find the area of the shaded region (circle minus square).
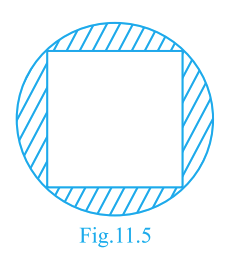
Answer:
\(16\pi - 32\;\text{cm}^2\) (≈ 18.27 cm² if \(\pi=3.14\))
Open
Question. 3
Find the area of a sector of a circle of radius 28 cm and central angle \(45^\circ\).
Answer:
\(98\pi\;\text{cm}^2\) (≈ 307.88 cm²)
Open
Question. 4
The radius of a motorcycle wheel is 35 cm. How many revolutions per minute must it make to keep a speed of 66 km/h?
Answer:
500 rpm
Open
Question. 5
A cow is tied with a rope 14 m long at the corner of a rectangular field of dimensions 20 m × 16 m. Find the area it can graze.
Answer:
\(49\pi\;\text{m}^2\) (≈ 153.94 m²)
Open
Question. 6
Find the area of the flower bed with semicircular ends shown in Fig. 11.6. The overall length is 38 cm and the overall width is 10 cm.
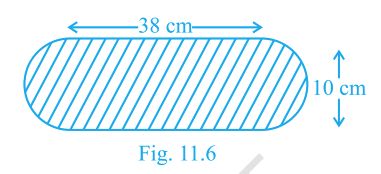
Answer:
\(280 + 25\pi\;\text{cm}^2\) (≈ 358.50 cm²)
Open
Question. 7
In Fig. 11.7, AB is a diameter of the circle, AC = 6 cm and BC = 8 cm. Find the area of the shaded region (use \(\pi = 3.14\)).
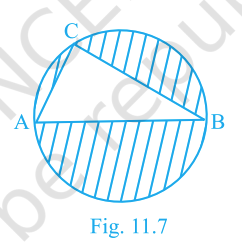
Answer:
54.5 cm²
Open
Question. 8
Find the area of the shaded field shown in Fig. 11.8. (Top width 8 m, left height 6 m with a semicircular bulge, right height 4 m with a semicircular bulge.)
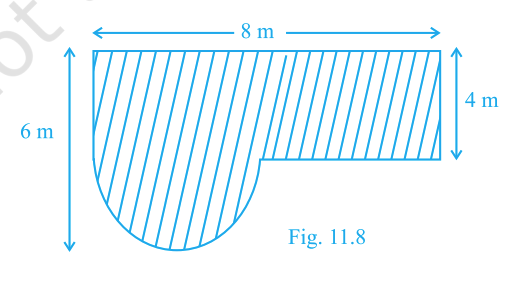
Answer:
\(32 + 6.5\pi\;\text{m}^2\) (≈ 52.42 m²)
Open
Question. 9
Find the area of the shaded region in Fig. 11.9 (outer rectangle 26 m × 12 m; inner 'stadium' has total length 20 m and width 4 m).
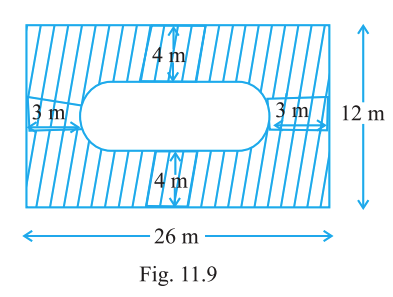
Answer:
\(248 - 4\pi\;\text{m}^2\) (≈ 235.43 m²)
Open
Question. 10
Find the area of the minor segment of a circle of radius 14 cm when the angle of the corresponding sector is \(60^\circ\).
Answer:
\(\dfrac{98\pi}{3} - 49\sqrt{3}\;\text{cm}^2\) (≈ 21.99 cm²)
Open
Question. 11
In Fig. 11.10 (square of side 12 cm), arcs with centres at \(A,B,C,D\) and radius 6 cm pass through the midpoints of adjacent sides, forming a central shaded region. Find the shaded area (use \(\pi=3.14\)).
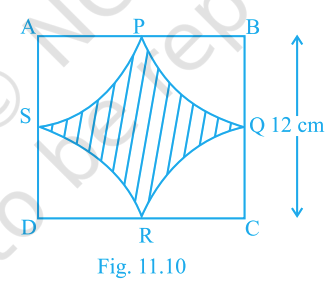
Answer:
\(144 - 36\pi\;\text{cm}^2\;\approx 30.96\,\text{cm}^2\)
Open
Question. 12
In Fig. 11.11, an equilateral triangle \(ABC\) of side 10 cm has arcs centred at \(A,B,C\) that meet sides at their midpoints \(D,E,F\). Find the area of the shaded central region (use \(\pi=3.14\)).
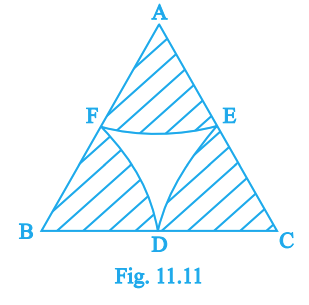
Answer:
\(25\sqrt{3} - \dfrac{25\pi}{2}\;\text{cm}^2\) (≈ 3.04 cm²)
Open
Question. 13
In Fig. 11.12, arcs are drawn with radii 14 cm and with centres at the triangle’s vertices \(P, Q, R\). Find the area of the shaded regions near the vertices.
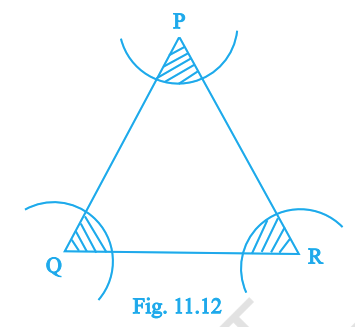
Answer:
\(98\pi\;\text{cm}^2\) (≈ 307.88 cm²)
Open
Question. 14
A circular park is surrounded by a road 21 m wide. If the park’s radius is 105 m, find the area of the road.
Answer:
\(4851\pi\;\text{m}^2\) (≈ 15{,}226.1 m²)
Open
Question. 16
A piece of wire 20 cm long is bent into an arc of a circle subtending an angle of \(60^\circ\) at the centre. Find the radius of the circle.
Answer:
\(\dfrac{60}{\pi}\;\text{cm}\) (≈ 19.10 cm)