NCERT Exemplar Solutions
Class 10 - Mathematics - CHAPTER 12: Surface Areas & VolumesExercise 12.3
Class 10 - Mathematics - CHAPTER 12: Surface Areas & Volumes
Question. 1
Three metallic solid cubes whose edges are 3 cm, 4 cm and 5 cm are melted and formed into a single cube. Find the edge of the cube so formed.
Answer:
6 cm
Open
Question. 2
How many shots each having diameter 3 cm can be made from a cuboidal lead solid of dimensions 9 cm \(\times\) 11 cm \(\times\) 12 cm?
Answer:
84 shots
Open
Question. 3
A bucket is in the form of a frustum of a cone and holds 28.490 litres of water. The radii of the top and bottom are 28 cm and 21 cm, respectively. Find the height of the bucket.
Answer:
15 cm
Open
Question. 4
A cone of radius 8 cm and height 12 cm is divided into two parts by a plane through the mid-point of its axis parallel to its base. Find the ratio of the volumes of the two parts.
Answer:
1 : 7
Open
Question. 5
Two identical cubes each of volume \(64\,\text{cm}^3\) are joined together end to end. What is the surface area of the resulting cuboid?
Answer:
160 cm²
Open
Question. 6
From a solid cube of side 7 cm, a conical cavity of height 7 cm and radius 3 cm is hollowed out. Find the volume of the remaining solid.
Answer:
\(343-21\pi\;\text{cm}^3\) (≈ 277.0 cm³)
Open
Question. 7
Two cones with same base radius 8 cm and height 15 cm are joined together along their bases. Find the surface area of the shape so formed.
Answer:
\(272\pi\;\text{cm}^2\)
Open
Question. 8
Two solid cones \(A\) and \(B\) are placed in a cylindrical tube as shown.
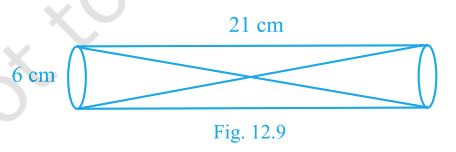
The ratio of their capacities is \(2:1\). Find the heights and capacities of the cones. Also find the volume of the remaining portion of the cylinder (tube length 21 cm, inner diameter 6 cm).
Answer:
Heights: \(14\,\text{cm}\) and \(7\,\text{cm}\).
Capacities: \(42\pi\,\text{cm}^3\) and \(21\pi\,\text{cm}^3\).
Remaining cylinder volume: \(126\pi\,\text{cm}^3\).
Open
Question. 9
An ice-cream cone with hemispherical top has radius 5 cm and height 10 cm (see figure).
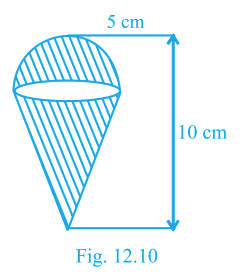
Calculate the volume of ice cream, if \(\dfrac16\) of the cone part is left unfilled.
Answer:
\(\displaystyle \dfrac{1375}{9}\pi\;\text{cm}^3\;\approx 4.80\times10^2\,\text{cm}^3\)
Open
Question. 10
Marbles of diameter 1.4 cm are dropped into a cylindrical beaker of diameter 7 cm containing some water. Find the number of marbles so that the water level rises by 5.6 cm.
Answer:
150 marbles
Open
Question. 11
How many spherical lead shots each of diameter 4.2 cm can be obtained from a solid rectangular lead piece of dimensions 66 cm, 42 cm and 21 cm?
Answer:
1500 shots
Open
Question. 12
How many spherical lead shots of diameter 4 cm can be made out of a solid cube of lead whose edge measures 44 cm?
Answer:
2541 shots
Open
Question. 13
A wall 24 m long, 0.4 m thick and 6 m high is constructed with bricks each of dimensions 25 cm \(\times\) 16 cm \(\times\) 10 cm. If the mortar occupies \(\dfrac{1}{10}\) of the volume of the wall, find the number of bricks used.
Answer:
12,960 bricks
Open
Question. 14
Find the number of metallic circular discs with 1.5 cm base diameter and height 0.2 cm to be melted to form a right circular cylinder of height 10 cm and diameter 4.5 cm.
Answer:
450 discs