NCERT Exemplar Solutions
Class 10 - Mathematics - CHAPTER 9: CirclesExercise 9.1
Class 10 - Mathematics - CHAPTER 9: Circles
Question. 1
1. If radii of two concentric circles are 4 cm and 5 cm, then the length of each chord of one circle which is tangent to the other circle is
3 cm
6 cm
9 cm
1 cm
Open
Question. 2
2. In Fig. 9.3, if \(\angle AOB = 125^\circ\), then \(\angle COD\) is equal to
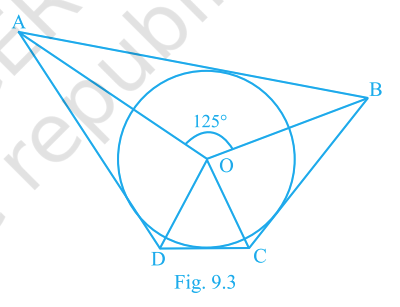
\(62.5^\circ\)
\(45^\circ\)
\(35^\circ\)
\(55^\circ\)
Open
Question. 3
3. In Fig. 9.4, \(AB\) is a chord and \(AOC\) is a diameter with \(\angle ACB=50^\circ\). If \(AT\) is tangent at \(A\), then \(\angle BAT\) equals
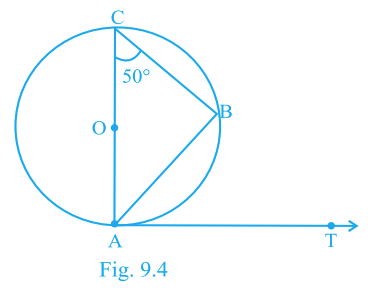
\(65^\circ\)
\(60^\circ\)
\(50^\circ\)
\(40^\circ\)
Open
Question. 4
4. From a point \(P\) at a distance 13 cm from the centre \(O\) of a circle of radius 5 cm, tangents \(PQ\) and \(PR\) are drawn. The area of quadrilateral \(PQOR\) is
\(60\,\text{cm}^2\)
\(65\,\text{cm}^2\)
\(30\,\text{cm}^2\)
\(32.5\,\text{cm}^2\)
Open
Question. 5
5. At one end \(A\) of a diameter \(AB\) of a circle of radius 5 cm, a tangent \(XAY\) is drawn. The length of the chord \(CD\) parallel to \(XY\) and at a distance 8 cm from \(A\) is
4 cm
5 cm
6 cm
8 cm
Open
Question. 6
6. In Fig. 9.5, \(AT\) is a tangent to the circle with centre \(O\) such that \(OT=4\) cm and \(\angle OTA=30^\circ\). Then \(AT\) equals
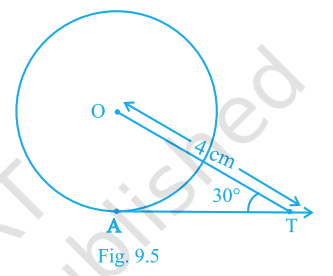
4 cm
2 cm
\(2\sqrt{3}\) cm
\(4\sqrt{3}\) cm
Open
Question. 7
7. In Fig. 9.6, if \(O\) is the centre, \(PQ\) a chord and the tangent \(PR\) at \(P\) makes \(50^\circ\) with \(PQ\), then \(\angle POQ\) is
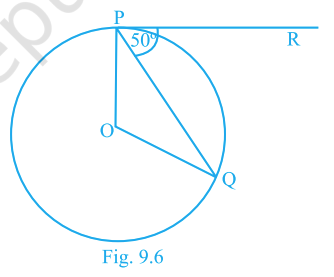
\(100^\circ\)
\(80^\circ\)
\(90^\circ\)
\(75^\circ\)
Open
Question. 8
8. In Fig. 9.7, if \(PA\) and \(PB\) are tangents from \(P\) and \(\angle APB=50^\circ\), then \(\angle OAB\) equals
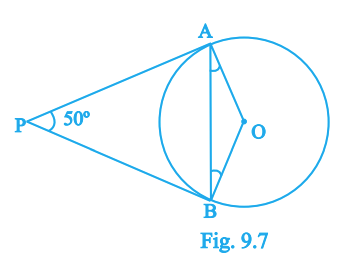
\(25^\circ\)
\(30^\circ\)
\(40^\circ\)
\(50^\circ\)
Open
Question. 9
9. If two tangents inclined at \(60^\circ\) are drawn to a circle of radius 3 cm, then the length of each tangent is
\(\dfrac{3}{2}\sqrt{3}\) cm
6 cm
3 cm
\(3\sqrt{3}\) cm
Open
Question. 10
10. In Fig. 9.8, if \(PQR\) is the tangent at \(Q\) (centre \(O\)), \(AB\) is a chord parallel to \(PR\) and \(\angle BQR=70^\circ\), then \(\angle AQB\) equals
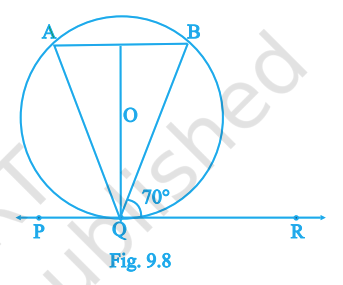
\(20^\circ\)
\(40^\circ\)
\(35^\circ\)
\(45^\circ\)